第 05 章：函数的定义

主要知识点：

• 利用已有函数定义新函数 / 条件表达式 / 模式匹配 / Lambda表达式 / Section

01 利用已有函数定义新函数

问题 1：判断一个整数是否是偶数

even :: Int -> Bool
even n = mod n 2 == 0

• 其中，mod 是一个已经存在的函数

问题 2：计算一个浮点数的倒数

recip :: Double -> Double
recip x  =  1 / x

• 其中，(/) 是一个已经存在的函数

问题 3：将一个 list 在位置 n 分开

splitAt :: Int -> [a] -> ([a], [a])
splitAt n xs  =  (take n xs, drop n xs)

• 其中，take 和 drop 是两个已经存在的函数

02 条件表达式 (Conditional Expression)

如同大多数编程语言一样，Haskell 中也存在 条件表达式

abs :: Int -> Int
abs n  =  if n >= 0 then n else -n

• 函数 abs
  • 接收一个整数 n
  • 如果 n 是一个非负值，则返回 n；否则，返回 -n

条件表达式可以被嵌套

signum :: Int -> Int
signum n  =  if n < 0 then -1 else
             if n == 0 then 0 else 1

• 在第一个条件表达式的 else 分支中，又嵌套了一个条件表达式

在 Haskell 中，不存在 三分支或更多分支的条件表达式

• 但通过条件表达式的嵌套，可以表达出三分支/多分支的语义

在 Haskell 中，不存在 单分支条件表达式

• 在 Rust 中，在语法上确实存在单分支条件表达式，但在语义上它仍然是一个双分支表达式

03 Guarded Equation

在定义函数时，也可以通过 Guarded Equation 语法实现多分支的效果：

abs :: Int -> Int
abs n | n >=    0  =   n
      | otherwise  =  -n

• 对于函数应用 abs n，

  • 当条件 n >= 0 成立时，abs n 被定义为 n
  • 当条件 otherwise 成立时，abs n 被定义为 -n

• otherwise 是 Prelude 模块输出的一个元素，其定义为 otherwise = true

• 因此，| otherwise = -n 是一个兜底的分支

signum :: Int -> Int
signum n | n < 0      = -1
         | n == 0     =  0
         | otherwise  =  1

• 显然，Guarded Equation 用来表达多分支结构，太方便了

04 模式匹配 (Pattern Matching)

很多函数更适合使用模式匹配进行定义：

not :: Bool -> Bool
not False  =  True
not True   =  False

• 这是模式匹配的一种极简形式，所以看起来有些无聊

  即便如此，如果不使用模式匹配，你能用其他方法定义 not 函数吗？

• 为什么这种定义方式称为模式匹配呢？解释如下：

  1. Bool 是 Prelude 模块输出的一个类型，其定义如下：

     data Bool = True | False
     

     • data 是 Haskell 语言中定义类型的关键字

     • 这个类型定义，用 “第二章：初见函数式思维” 中的那种语言，可以表述为如下形式：

       def Bool : Type = {
           ctor True  : Self,
           ctor False : Self,
       }
       

     • 也即，类型 Bool 的值仅存在两种模式 / 构造方式 / Constructor

  2. 因此，如果在这两种模式上对 not 给出了定义，自然地，就给出了 not 的完整定义

• 称上面的模式匹配是一种极简形式，原因是：

  • 其中涉及的两个模式 True False 没有参数

    • 在更一般的情况下，模式中存在参数；然后，就会很有趣

• 在更本质的意义上，“模式匹配” 就是 分情况讨论

利用模式匹配，定义 逻辑与 函数。三种方式：

-- 方式一
(&&) :: Bool -> Bool -> Bool
True  && True  = True
True  && False = False
False && True  = False
False && False = False

-- 方式二
(&&) :: Bool -> Bool -> Bool
True  && True  = True
_     && _     = False

• 下划线 _ 是一个通配符，可以匹配到任何值

• 上面的程序表明：模式匹配的顺序存在语义

  • 即：按照定义中出现的模式匹配语句依次进行匹配

-- 方式三
(&&) :: Bool -> Bool -> Bool
True  && b = b
False && _ = False

• 与前两种定义方式相比，这种方式具有更高的效率

  • 原因：它完全避免了对第二个参数的评估

• 在第一个模式匹配语句中出现的 b， 称为 变量模式

  • 它的效果：把第二个参数绑定到局部变量 b 上

Haskell 不支持在一个模式匹配语句中出现两个相同的变量模式。

例如，如下定义存在编译时错误：

(&&) :: Bool -> Bool -> Bool
b && b = b
_ && _ = False

• 在表面上看起来，这样的程序似乎没有问题

• 但在一般的意义上，判断两个东西是否相等，存在理论或技术上的困难性

05 序列模式 (List Pattern)

List 类型的定义如下：

data List a = [] | (:) a (List a)

其中，出现了两个模式 / 构造方式 / Constructor：

1. []：其类型为 List a
2. (:)：其类型为 a -> List a -> List a

Haskell 支持采用如下语法表达一个 list：

• [1, 2, 3, 4, 5]

这实际上是一种语法糖，去糖后，得到的表达式如下：

• 1 : (2 : (3 : (4 : (5 : []))))

然后，Haskell 规定：运算符 : 满足右结合律。因此，该表达式可进一步简化为：

• 1 : 2 : 3 : 4 : 5 : []

删除空格后，得到更为紧凑的形式：

• 1:2:3:4:5:[]

定义 List 上的函数时，一种常见的模式是 x:xs。其效果是：

• 把一个 list 的第一个元素 绑定到 局部变量 x 上

• 把一个 list 删除第一个元素后得到的 list 绑定到 局部变量 xs 上

以下为两个示例函数：

head :: [a] -> a
head (x:_)  =  x

tail :: [a] -> [a]
tail (_:xs)  =  xs

• 只有非空 list 才能匹配到模式 x:xs 上

  • 因此，这两个函数都是 partial function (它们在 [] 上没有定义)

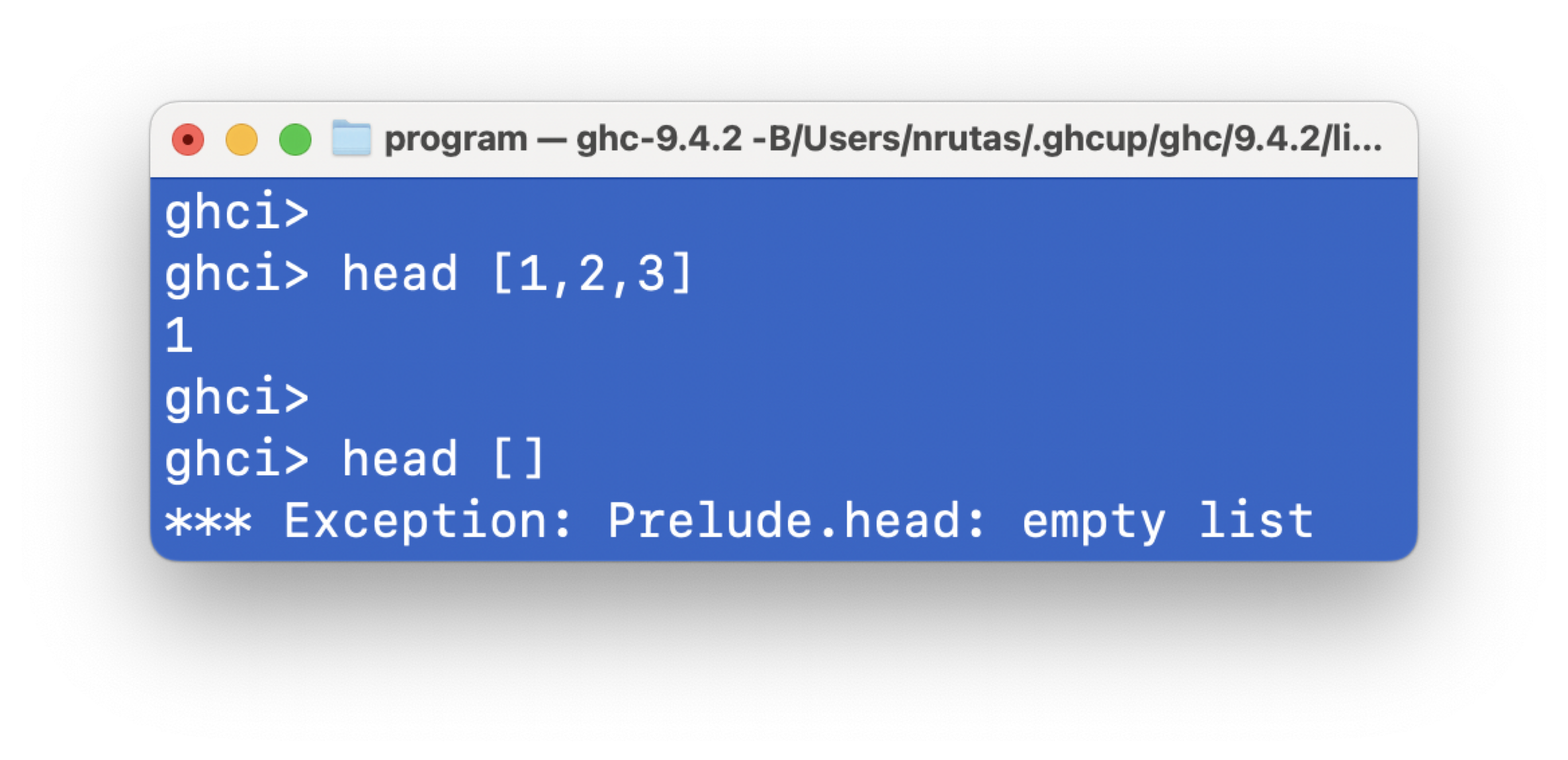
注意：以下程序会产生编译错误：

head :: [a] -> a
head x:_  =  x

原因：

• 在 Haskell 中，function application (函数应用) 具有最高优先级

• 因此，head x:_ = x 会被编译器理解为 (head x):_ = x

06 元组模式 (Tuple Pattern)

元组模式没有什么好说的，仅以两个示例意思一下：

-- Extract the first component of a pair.
fst :: (a, b) -> a
fst (x, _)  =  x

-- Extract the second component of a pair.
snd :: (a, b) -> b
snd (_, y)  =  y

07 λ 表达式 (Lambda Expression)

在非常肤浅的层面上，λ 表达式提供了如下能力：

• 创建匿名函数：即，创建一个没有名字的函数

例如：表达式 \x -> x + x 是一个匿名函数

• 该函数接收一个 x，返回 x + x

可以把 λ 表达式中的左斜线 \ 理解为字母 λ 的 谐形字母

• 为什么要这样呢？
• 原因：键盘输入 λ 不方便

λ 表达式 为柯里化函数的定义提供了更加精确的含义

• 例如：add x y = x + y，其含义是：

• add = \x -> (\y -> x + y)

λ 表达式 可对仅使用一次的函数进行 “匿名原地构造”

odds n = map f [0..n-1]
  where
    f x = x * 2 + 1

-- defined in Prelude
map :: (a -> b) -> [a] -> [b]
map _ []  =  []
map f (x:xs)  =  f x : map f xs

• 在上面的程序中，odds函数的定义中，出现了一个仅使用了一次的函数 f

• 可以使用 λ 表达式 在使用的地方对该函数进行匿名原地构造

  odds n = map (\x -> x * 2 + 1) [0..n-1]
  

08 Operator Sections

把一个二元运算符放在一对圆括号中，就能得到该运算符对应的柯里化函数

ghci> 1 + 2
3
ghci> (+) 1 2
3
ghci> :type (+)
(+) :: Num a => a -> a -> a

甚至可以在圆括号中放置一个参数

ghci> (+ 1) 2
3
ghci> :type (+ 1)
(+ 1) :: Num a => a -> a

ghci> (1 +) 2
3
ghci> :type (1 +)
(1 +) :: Num a => a -> a

ghci> (1 -) 2
-1
ghci> :type (1 -)
(1 -) :: Num a => a -> a

但是，存在一个特殊情况

ghci> :type (- 1)
(- 1) :: Num a => a
ghci> (- 1) 2
<interactive>:5:1: error: [GHC-39999]

• 其中，- 1 被编译器理解为对 1 取负数

在一般意义上，对于任意二元运算符 ⊕，如下三种形式称为 “section”

• (⊕)，(x ⊕)，(⊕ y)

这三种 section 的定义如下：

• (⊕) === \x -> (\y -> x ⊕ y)

• (x ⊕) === \y -> x ⊕ y

• (⊕ y) === \x -> x ⊕ y

使用 section，可以方便地定义一些函数

• (+ 1)：后继函数

• (1 /)：倒数函数

• (* 2)：翻倍函数

• (/ 2)：减半函数

本章作业

作业 01

定义一个 safetail 函数，满足如下要求：

1. 该函数与 tail 函数具有相同的类型
2. 当作用在一个非空 list 上，该函数与 tail 行为相同
3. 当作用在一个空 list 上，该函数返回一个空 list

说明：

• 如果你愿意，可以使用函数 null :: [a] -> Bool 判断 list 是否为空

作业 02

Luhn 算法被用于检查银行卡号中可能存在的简单书写错误 (例如，写错了一个数字)。

该算法的工作流程如下所述：

1. 将银行卡号中的每一个数字字符视为一个独立的整数
2. 从右向左，偶数位的数乘 2 (奇数位的数不变)
3. 对于每一个大于 9 的数，减去 9；然后将所有的数相加
4. 如果相加的结果能被 10 整除，则表示银行卡号合法；否则，非法

定义函数 luhn :: Int -> Int -> Int -> Int -> Int，对 4 位卡号的合法性进行检查。例如：

ghci> luhn 1 7 8 4
True

ghci> luhn 4 7 8 3
False