第 01 章:课程简介
课程名称:计算概论A (实验班) - 函数式程序设计
授课教师:胡振江,张伟
开课单位:信息科学技术学院 / 计算机学院
开课时间:2025 年 09 ~ 12 月
本文档的内容为课程课件;未经允许,请勿用做商业用途。
第 02 章:初见函数式思维
01 两句很有哲理的话
-
工欲善其事,必先利其器。
-
To a man with a hammer, everything looks like a nail.
- 思维方式是一种工具;不能被思维方式束缚
02 “函数式思维” 是一种什么样的思维方式
-
使用 “数学中的函数” 作为 求解信息处理问题的基本成分。
-
“使用方式” 包括:
-
从零开始,定义一些基本函数
-
把已有的函数组装起来,形成新的函数
-
03 简要回顾:数学中的函数
定义: 函数 / Function
对任何两个集合
X和Y,称两者之间的关系f ⊆ X ✗ Y是一个函数,当且仅当如下条件成立:
∀ x ∈ X, ∃ (u, v) ∈ f, x = u∀ (x, y) ∈ f, ∀ (u, v) ∈ f, x = u => y == v也即:对
X中的任何元素x,存在且仅存唯一一个元素y ∈ Y,满足(x, y) ∈ f
函数相关的表示符号:
对任何两个集合X和Y,
-
X ✗ Y-
一个集合,其定义为:
{ (x, y) | x ∈ X, y ∈ Y } -
也称为集合
X和Y的 笛卡尔积
-
-
X -> Y- 一个集合,包含且仅包含所有从
X到Y的函数
- 一个集合,包含且仅包含所有从
-
f : X -> Y-
声明
f是一个从X到Y的函数。也称:f是一个类型为X -> Y的函数 -
称:
X为f的定义域 (Domain);Y为f的值域 (Codomain)
-
-
f(x)-
函数
f的定义域中元素x映射到的值域中的那个元素, -
显然可知:
-
f(x) : Y,也即:f(x)的类型为Y -
(x, f(x)) ∈ f
-
-
常用的集合及其表示符号:
在 Haskell 中,“类型” 和 “集合” 是同义词
-
ℕ:自然数集合/类型 -
ℤ:整数集合/类型 -
ℚ:有理数集合/类型 -
ℝ:实数集合/类型 -
𝔹 = { true, flse }:布尔集合/类型。其中,-
true表示 “真”;flse表示 “假” -
稍后给出
𝔹的一种更为形式化的定义
-
定义: 函数的组合 / Function Composition
对任何两个函数
f : X -> Y、g : Y -> Z,两者的组合,记为g * f,是一个函数。该函数的定义如下:
[ X Y Z : Set, f : X -> Y, g : Y -> Z ] def g * f : X -> Z = [x : X] g(f(x))说明:
上述定义不是采用 Haskell 语言书写的程序
本章中出现的所有程序 (除了最后一个),都不是 Haskell 程序
- 这些程序所采用的语法,来源于我们正在设计中的一种用于数学证明的语言
04 为什么在函数的基础上,可以形成一种思维方式
-
函数可以建模 “变换” 和 “因果关系”
-
信息处理问题,本质上是一种信息的变换问题
-
在面向特定领域问题的软件应用中,大量涉及对物理世界中因果关系的仿真
-
05 几个简单的函数
-
逻辑非函数
def not : 𝔹 -> 𝔹 = [b] match b { true => flse, flse => true, } -
逻辑与函数
def and : (𝔹 ✗ 𝔹) -> 𝔹 = [p] match p { (true, true) => true, _ => flse, }另一种定义方式:
def and : 𝔹 -> 𝔹 -> 𝔹 = [l] [r] match (l, r) { (true, true) => true, _ => flse, } -
为了定义关于自然数
ℕ的函数,我们首先需要给出ℕ的定义def ℕ : Type = { ctor zero : Self ctor succ : Self -> Self }这是一种递归定义,其含义如下:
-
zero是ℕ中的一个元素 -
如果
n是ℕ中的一个元素,那么,succ n也是ℕ中的一个元素 -
ctor是一个关键字 (Key Word),其英文单词 “constructor” 的缩写-
ctor后面的那个元素是一个公理 (无需给出元素的定义)- 所谓公理,就是一个神秘存在
-
为什么可以这样定义自然数呢?
因为在这种定义下,我们可以做出如下设定:
0 === zero1 === succ(zero)2 === succ(succ(zero))3 === succ(succ(succ(zero)))
小和尚:
- 这不就是上古传说中的 “结绳记数” 吗!
唐僧:
- 思维真敏捷;真是一个值得教育的好孩子!
小和尚:
- 但是,这么 low 的自然数定义,真的适合在北京大学的课堂上讲吗?
唐僧:
-
我猜测,也许你的思维被你的高中数学老师囚禁在数学宇宙的一片荒漠中了
-
采用类似的方式,我们也可以对
𝔹给出形式化的定义def 𝔹 : Type = { ctor flse : Self, ctor true : Self, }
-
-
自然数的加法运算
def plus : ℕ -> (ℕ -> ℕ) = [a] [b] match (a, b) { (m, zero) => m, (m, succ(n)) => succ(plus(m)(n)) }加法运算示例:
plus(3)(4) -- 因为实在受不了“结绳记数”的自然数,所以局部回归人类世俗文明😅 === plus(3)(succ(3)) === succ(plus(3)(3)) === succ(plus(3)(succ(2))) === succ(succ(plus(3)(2))) === succ(succ(plus(3)(succ 1))) === succ(succ(succ(plus(3)(1)))) === succ(succ(succ(plus(3)(succ 0)))) === succ(succ(succ(succ(plus(3)(0))))) === succ(succ(succ(succ(3)))) === (succ * succ * succ * succ)(3)不要被上面这种看似复杂的定义所困扰。
它只不过用递归的方式定义了一件很简单的事情:
plus(m)(n) === (succ * succ * succ * ... * succ)(m) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "the composition of n succ" -
自然数的乘法运算
def mult : ℕ -> (ℕ -> ℕ) = [a] [b] match (a, b) { (m, zero) => zero, (m, succ(n)) => plus(m)(mult(m)(n)) }乘法运算示例:
mult(3)(4) === mult(3)(succ 3) === plus(3)(mult(3)(3)) === plus(3)(mult(3)(succ 2)) === plus(3)(plus(3)(mult(3)(2))) === plus(3)(plus(3)(mult(3)(succ 1))) === plus(3)(plus(3)(plus(3)(mult(3)(1)))) === plus(3)(plus(3)(plus(3)(mult(3)(succ 0)))) === plus(3)(plus(3)(plus(3)(plus(3)(mult(3)(0))))) === plus(3)(plus(3)(plus(3)(plus(3)(0)))) === (plus(3) * plus(3) * plus(3) * plus(3))(0)不要被上面这种看似复杂的定义所困扰。
它只不过用递归的方式定义了一件很简单的事情:
mult(m)(n) === (plus(m) * plus(m) * ... * plus(m))(zero) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "the composition of n plus(m)" -
自然数的指数运算
def expn : ℕ -> (ℕ -> ℕ) = [a] [b] match (a, b) { (m, zero) => succ(zero), (m, succ(n)) => mult(m)(expn(m)(n)) }指数运算示例:
expn(3)(4) === expn(3)(succ 3) === mult(3)(expn(3)(3)) === mult(3)(expn(3)(succ 2)) === mult(3)(mult(3)(expn(3)(2))) === mult(3)(mult(3)(expn(3)(succ 1))) === mult(3)(mult(3)(mult(3)(expn(3)(1)))) === mult(3)(mult(3)(mult(3)(expn(3)(succ 0)))) === mult(3)(mult(3)(mult(3)(mult(3)(expn(3)(0))))) === mult(3)(mult(3)(mult(3)(mult(3)(1)))) === (mult(3) * mult(3) * mult(3) * mult(3))(1)不要被上面这种看似复杂的定义所困扰。
它只不过用递归的方式定义了一件很简单的事情:
expn(m)(n) === (mult(m) * mult(m) * ... * mult(m))(succ(zero)) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "the composition of n mult(m)"小和尚:
- 总是n个相同函数的组合;能不能有些新东西呢?
唐僧:
- 何必让自己这么累;这样划水不挺好嘛!
-
阶乘运算
def fact : ℕ -> ℕ = [m] match m { zero => succ(zero), succ(n) => mult(succ(n))(fact(n)), }不要被上面这种看似复杂的定义所困扰
它只不过用递归的方式定义了一件很简单的事情:
fact(m) === (mult(m) * mult(m - 1) * ... * mult(1))(1) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "the composition of n mult(_)"唐僧: 看,是不是有那么一点点新东西了 😅
-
斐波那契函数
def fib : ℕ -> ℕ = [m] match m { zero => zero, succ(zero) => succ(zero), succ(succ(n)) => plus(fib(n))(fib(succ n)), }斐波那契函数运算示例:
fib(5) === plus(fib(3))(fib(4)) === plus(plus(fib(1))(fib(2)))(plus(fib(2))(fib(3))) === plus(plus(1)(plus(fib(0))(fib(1))))(plus(plus(fib(0))(fib(1)))(plus(fib(1))(fib(2)))) === plus(plus(1)(plus(0)(1)))(plus(plus(0)(1))(plus(1)(plus(fib(0))(fib(1))))) === plus(plus(1)(plus(0)(1)))(plus(plus(0)(1))(plus(1)(plus(0)(1))))小和尚: 这下好了,没有规律了。看你怎么圆过来 😜
06 自然数上的 fold 函数
-
plusmultexpn这三个函数之间存在共性 -
这种共性可以被封装在一个函数中
[T : Type] def fold : (T -> T) -> (T -> (ℕ -> T)) = [h : T -> T] [c : T] [m : ℕ] match m { zero => c, succ n => h(fold(h)(c)(n)) } ------ 引入一点语法糖 ------ = [h : T -> T, c : T, m : ℕ] match m { zero => c, succ n => h(fold(h)(c)(n)) } -
给定
h : T -> T,c : T,令f === fold(h)(c),则可知:-
f(zero) === c -
f(succ n) === h(f(n))
-
-
如果不理解这个定义的含义,请看如下解释:
给定一个自然数
n,可知:n === (succ * succ * succ * ... * succ)(zero) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "the composition of n succ"已知
f === fold(h)(c),则可知:f(n) === ( h * h * h * ... * h )(c) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "the composition of n h"也即:
-
f(n)把n中的zero替换为c,把每一个succ替换为h -
n和f(n)是同构的,即:两者具有相同的结构
-
-
使用
fold函数,可以对plusmultexpn这三个函数进行更深刻的定义def plus : ℕ -> (ℕ -> ℕ) = [m] fold(succ)(m) def mult : ℕ -> (ℕ -> ℕ) = [m] fold(plus(m))(zero) def expn : ℕ -> (ℕ -> ℕ) = [m] fold(mult(m))(succ(zero))示例:
----the composition of n succ ----- n === (succ * succ * ... * succ )(zero) | | | | | plus(m)(n) === (succ * succ * ... * succ )(m) | | | | | mult(m)(n) === (plus(m) * plus(m) * ... * plus(m))(zero) | | | | | expn(m)(n) === (mult(m) * mult(m) * ... * mult(m))(succ(zero)) -
使用
fold函数,也可以对factfib这两个函数进行更深刻的定义首先引入两个辅助函数:
[A B : Type] def fst : A ✗ B -> A = [(a, b)] a [A B : Type] def snd : A ✗ B -> B = [(a, b)] bfact函数的定义:def fact : ℕ -> ℕ = { def f : ℕ ✗ ℕ -> ℕ ✗ ℕ = [(m, n)] (m + 1, (m + 1) * n); ret snd * (fold(f)(0, 1)); }----the composition of n succ ---- n === ( succ * succ * ... * succ )(0) | | | | | | fact(n) === snd( ( f * f * ... * f )(0, 1) )fib函数的定义:def fib : ℕ -> ℕ = { def g : ℕ ✗ ℕ -> ℕ ✗ ℕ = [(m, n)] (n, m + n); ret fst * (fold(g)(0, 1)); }----the composition of n succ ---- n === ( succ * succ * ... * succ )(0) | | | | | | fib(n) === fst( ( g * g * ... * g )(0, 1) )
07 List 类型
-
在信息处理问题中,经常涉及一组按照某种顺序排列的数据;
我们将这类数据用 List 类型进行表示。
-
例如:对于排序问题
-
待排序的数据通常采用 List 的方式进行输入
-
排序的结果自然也以 List 的方式返回
-
-
-
List 类型的定义
def List : Type -> Type = [A] { ctor nil : Self, ctor (+>) : A -> Self -> Self, } -
List 类型的示例
-
List(ℕ):自然数序列类型 -
nil:一个不包含任何元素的空序列 -
1 +> nil:仅包含 1 个元素1的自然数序列 -
1 +> (2 +> (3 +> (4 +> nil))):包含 4 个元素1234的自然数序列
-
-
List 类型相关的函数
添加元素函数:
[T : Type] def cons : T -> (List(T) -> List(T)) = [x, xs] x +> xs -- 这个函数就是把运算符 +> 进行了函数化长度函数:
[T : Type] def len : List(T) -> ℕ = [xs] match xs { nil => 0, a +> yx => 1 + len(yx) }逆序函数:
[T : Type] def rev : List(T) -> List(T) = { def rev-memo : List(T) -> (List(T) -> List(T)) = [xs, ys] match ys { nil => xs, m +> ms => rev-memo(m +> xs)(ms), }; ret rev-memo(nil); }序列拼接函数:
[T : Type] def concat : List(T) -> (List(T) -> List(T)) = [xs, ys] match xs { nil => ys, m +> ms => m +> (concat(ms)(ys)), }过滤函数:
[T : Type] def filter : (T -> 𝔹) -> (List(T) -> List(T)) = [f, xs] match xs { nil => nil, m +> ms => match f(m) { true => m +> filter(f)(ms), flse => filter(f)(ms), } }
08 List 上的 fold 函数
-
如果我的理解没有错误,在任何类型上都存在 fold 函数
这个观点待确认。 数学上的事情,只要没有给出证明,都不能随意相信。 -
无论如何,
List类型上存在 fold 函数,而且存在两个。我们将这两个函数分别命名为
foldl和foldr。- 其中的后缀
l和r分别表示left和right
- 其中的后缀
-
foldr函数[A B : Type] def foldr : (A -> (B -> B)) -> (B -> (List(A) -> B)) = [h : A -> (B -> B), b : B, xs : List(A)] match xs { nil => b, a +> ys => h(a)(foldr(h)(b)(ys)) }如果不理解这个定义,请看如下解释:
-
给定
xs : List(A),不失一般性,令:xs === xn +> xn-1 +> ... +> x1 +> nil则可知:
xs === ( cons(xn) * cons(xn-1) * ... * cons(x1) )(nil) -
已知
f === foldr(h)(b),则可知:f(xs) === ( h(xn) * h(xn-1) * ... * h(x1) )(b) -
也即:
-
f(xs)把xs中的nil替换为b,把xs中的每一个cons替换为h -
xs和f(xs)是同构的,即:两者具有相同的结构
-
-
-
foldl函数[A B : Type] def foldl : (B -> (A -> B)) -> (B -> (List(A) -> B)) = [h : B -> (A -> B), b : B, xs : List(A)] match xs { nil => b, a +> ys => foldl(h)(h(b)(a))(ys), }如果不理解这个定义,请看如下解释:
-
引入一个工具函数
[A B C : Type] def flip : (A -> (B -> C)) -> (B -> (A -> C)) = [f, b, a] f a b -
给定
xs : List(A),不失一般性,令:xs === xn +> xn-1 +> ... +> x1 +> nil则可知:
xs === ( cons(xn) * cons(xn-1) * ... * cons(x1) )(nil) -
已知
f === foldr(h)(b),令h' = flip(h),则可知:f(xs) === ( h'(x1) * h'(x2) * ... * h'(xn) )(b) -
也即:
-
f(xs)把xs中的nil替换为b,把xs中的每一个cons替换为h' -
同时,还顺带逆序了一下
-
-
但实际上,并不存在一个显式的逆序环节;更真实的计算过程如下
f(xs) === b ≺ xn ≺ xn-1 ≺ ... ≺ x1 ≺ nil其中:运算符
≺具有左结合性,且b ≺ a === h(b)(a)
-
09 使用fold函数,重定义List相关的函数
-
len函数[A : Type] def len : List(A) -> ℕ = { def h : A -> ℕ -> ℕ = [_, n] n + 1; ret foldr(h)(0) }xs === ( cons(xn) * cons(xn-1) * ... * cons(x1) )(nil) len(xs) === ( h(xn) * h(xn-1) * ... * h(x1) )(0) -
rev函数[A : Type] def rev : List(A) -> List(A) = foldl(flip(cons))(nil) -
concat函数[A : Type] def concat : List(A) -> (List(A) -> List(A)) = [xs, ys] foldr(cons)(ys)(xs) -
filter函数[A : Type] def filter : (A -> 𝔹) -> (List(A) -> List(A)) = [f] { def h : (A -> 𝔹) -> (A -> (List(A) -> List(A))) = [f, a, xs] match f(a) { true => a +> xs, flse => xs, } ret foldr(h(f))(nil); }xs === ( cons(xn) * cons(xn-1) * ... * cons(x1) )(nil) filter(f)(xs) === ( h(f)(xn) * h(f)(xn-1) * ... * h(f)(x1) )(nil)
10 一种排序算法
-
快速排序算法
def qsort : List(ℕ) -> List(ℕ) = [xs] match { nil => nil, n +> ns => { def left = qsort(filter([m] m < n)(ns)); def rigt = qsort(filter([m] m >= n)(ns)); ret concat(left)(n +> rigt); } }小和尚:
- 这段代码看起来还不错 👍
唐僧:
-
你的审美能力看起来也不错 👏
-
可以让你看一下去年的形式:
qsort : List(ℕ) -> List(ℕ) qsort(nil) = nil qsort(n +> ns) = concat(concat(qsort(filter(lt(n))(ns)))([n]))(qsort(filter(ge(n))(ns))) where lt : ℕ -> (ℕ -> 𝔹) lt(n)(m) = if m < n then true else flse ge : ℕ -> (ℕ -> 𝔹) ge(n)(m) = not(lt(n)(m))
小和尚:
- 如果这就是用 FP 书写的算法,此生绝不学 FP!
唐僧:
- 好孩子,如果给你三生三世的财富,学否?
小和尚:
- 佛学工作者可是不能撒谎的哦!!!
-
内容 与 形式
-
这是一个关于 “内容” 与 “形式” 两者之间关系的问题
-
内容:对自然数序列进行排序的一种方法
-
形式:表现这种排序方法的形式
-
-
进一步而言,去年的程序存在的问题可以表述为:
- “形式” 小于 “内容”: 内容是很好的,但形式实在是太糟糕了
-
如果你能体会到这一点,你会发现:这个问题的严重程度并不像表面上看起来的那样
-
为什么这么说呢?因为,本质(内容)毕竟还是很好的
-
-
重走长征路
-
在某种意义上,我们正在“重走长征路”
-
在很多年以前,科研工作者们就已经意识到了这个问题
- 即:函数式思维的 “形式” 小于 “内容”
-
在这个问题的驱使下,他/她们设计了各种各样的函数式程序设计语言
-
我们即将介绍的Haskell语言,就是这些函数式程序设计语言的集大成者
-
不过,目前看来,Haskell 语言正在老去:一鲸落,万物生!
- 例如,本章中程序的语法,就是在 Haskell 语言的基础上改良形成的
-
11 剧透:采用 Haskell 语言编写的 qsort 算法
qsort :: Ord a => [a] -> [a]
qsort [] = []
qsort (p:xs) = qsort lt ++ [p] ++ qsort ge
where
lt = filter (< p) xs
ge = filter (>= p) xs
本章作业
本章没有作业。
但是,你需要想清楚:这门课是否适合你。
第 03 章:初见 Haskell
使用 Haskell 语言定义函数
在这一节中,我们采用 Haskell 语言,对上一章给出的若干函数示例进行重定义,并结合这些示例对 Haskell 语言的相关细节进行说明。
01 逻辑非运算
第 1 种定义方式:模式匹配 (Pattern Matching)
not :: Bool -> Bool
not True = False
not False = True
相关信息说明:
-
你可以在
https://play.haskell.org/这个页面实际运行一下这个程序在 Haskell 缺省加载的信息中已经存在了
not函数的定义;
为了避免重名导致的编译错误,最简单的调整方式:把函数名改变一下。尝试在
https://play.haskell.org/中输入如下程序:main :: IO () main = do putStrLn $ show $ not' True not' :: Bool -> Bool not' True = False not' False = True然后点击 “Run” 按钮
-
Bool是一个类型;它包含两个值:TrueFalse -
not :: Bool -> Bool:声明not的类型是Bool -> Bool小和尚: 为什么不用单个冒号
:作为类型声明符?唐僧: 在Haskell中,单冒号另有它同;
- 目前看来,“双冒号作为类型声明符” 这个设计决策并不好
-
not True = False:把not True这个表达式定义为False -
not False = True:把not False这个表达式定义为True
上述程序的一种轻微变体:
not :: Bool -> Bool
not x = case x of
True -> False
False -> True
第 2 种定义方式:条件表达式 (Conditional Expression)
not :: Bool -> Bool
not x = if x == True then False else True
相关信息说明:
-
在 Haskell 中,
=和==具有完全不同的含义-
=表示 “定义为”,即:将其左侧的表达式定义为右侧的表达式 -
==是一个 逻辑运算符,用来计算左右两侧表达式的值是否相等
-
第 3 种定义方式:Guarded Equations
not :: Bool -> Bool
not x | x == True = False
| x == False = True
或者,
not :: Bool -> Bool
not x | x = False
| otherwise = True
02 逻辑与运算
第 1 种定义方式:Pattern Matching
and :: Bool -> Bool -> Bool
and True True = True
and True False = False
and False True = False
and False False = False
相关信息说明:
-
在 Haskell 中,运算符
->满足右结合律- 也即:
Bool -> Bool -> Bool等价于Bool -> (Bool -> Bool)
思考:
(Bool -> Bool) -> Bool这个类型的含义是什么? - 也即:
第 2 种定义方式:Pattern Matching + Wildcard
and :: Bool -> Bool -> Bool
and True True = True
and _ _ = False
- 一个单独的下划线
_是一个 wildcard,表示这里有一个值,但我们选择无视它
作业 01
关于逻辑与 (and) 函数,你还能想到其他定义方式吗?
请用 Haskell 语言写出至少其他三种定义方式。
更传统的一种定义方式
and :: (Bool, Bool) -> Bool
and (True, True) = True
and (_ , _ ) = False
03 整数的算术运算
算术运算符
在书写算术运算时,通常不会采用函数的形式进行书写,而是采用更为直观的算术运算符 (Operator)
- 例如,一般不会书写
plus a b,而是写为a + b
Haskell 提供了常用的算术运算符:
+加法运算;-减法运算;*乘法运算;^指数运算
二元运算符的函数化
对于两个整数 x y:
-
x + y===(+) x y -
也即,
(+)是一个函数,其类型为Integer -> Integer -> Integer -
Integer是 Haskell 提供的一种整数类型,可以表示任意整数值
在此基础上,Haskell还提供了一种增强语法
-
(x +) y===x + y -
(+ y) x===x + y
函数的运算符化
对于一个函数,也可以将其转换为对应的运算符:
- 例如,
div x y===x`div`y
整数的除运算
-
如果你需要的是整除运算,使用函数
div -
如果你需要的是带有小数的除运算,使用运算符
/
作业 02
请用目前介绍的 Haskell 语言知识,给出函数
div的一种或多种定义。
- div :: Integer -> Integer -> Integer
说明:
不用关注效率
不用关注第二个参数为 0 的情况
如果你认为这个问题无解或很难,请给出必要的说明
- 为什么无解? 或者,困难在哪里?
04 自然数相关的函数
自然数类型
Haskell 标准库的模块Numeric.Natural中定义了一种自然数类型Natural,可表示任意自然数。
但这个类型缺省没有被加载到程序中。
为了在程序中使用这个类型,我们需要在程序文件的开始添加如下语句:
import Numeric.Natural (Natural)
- 含义:把
Numeric.Natural模块中的元素Natural引入到当前程序文件中
阶乘函数
fact :: Natural -> Natural
fact 0 = 1
fact n = n * fact (n - 1)
-
这是一个采用 pattern matching 进行定义的函数,含义如下:
- 对于一个自然数
n:- 如果
n == 0,则将fact n定义为1 - 否则,将
fact n定义为n * fact (n - 1)
- 如果
- 对于一个自然数
-
在程序运行过程中,如果要评估表达式
fact x的值,则会按照定义中给出的顺序进行模式匹配。具体而言:
-
首先检查
x是否可以匹配到0上:若匹配成功,则将fact x评估为0;否则,继续匹配。 -
继续检查
x是否可以匹配到通配符n上。
因为:n是通配符,可以匹配到任何自然数上。
所以:这次匹配一定成功,从而将fact x评估为x * fact (x - 1)
-
-
在 Haskell 中,函数应用 (Function Application) 具有最高优先级
- 因此:
x * fact (x - 1)等价于x * (fact (x - 1))
- 因此:
作业 03
关于阶乘函数,你还能想到其他定义方式吗?
请分别使用 “guarded equations” 和 “conditional expression” 写出阶乘函数的定义。
自然数上的 fold 函数
fold :: (t -> t) -> t -> Natural -> t
fold h c 0 = c
fold h c n = h (fold h c (n - 1))
说明:
- 在
fold的类型中,小写字母t表示一个 类型变量,Natural表示一个具体的类型
小和尚:
- 如何确定函数类型声明中出现的名称,是一个具体类型,还是一个类型变量呢?
唐僧:
- 对于该问题,Haskell 在语法层次上给出了一种简单有效的解决方案:
- 如果名称的 首字符 是 小写字母,则表示 类型变量
- 如果名称的 首字符 是 大写字母,则表示 具体类型
-
表达式
h (fold h c (n - 1))中出现的圆括号不是:主流编程语言 (C/C++/Java/Rust) 中函数调用时用于传参的圆括号
而是:用于 调整运算顺序 的圆括号。
- 如果不加这些括号,则
h fold h c n - 1===((((h fold) h) c) n) - 1
- 如果不加这些括号,则
-
在 Haskell 中:
-
函数调用具有最高优先级。因此,肯定比运算符的优先级高
-
函数调用满足左结合律。因此,
f g h k===((f g) h) k
-
-
如果你对这种调整运算顺序的括号很反感,Haskell 提供了另一种解决方案:
二元运算符:
$-
该运算符:1. 具有最低优先级;2. 满足右结合律
-
运算效果:把左侧的函数 应用到 右侧的元素上
因此,如下三个表达式等价:
h (fold h c (n - 1)) h $ fold h c (n - 1) h $ fold h c $ n - 1 -
阶乘函数 (fold版本)
fact :: Natural -> Natural
fact = snd . (fold f (0, 1))
fst :: (a, b) -> a
fst (x, _) = x
snd :: (a, b) -> b
snd (_, y) = y
f :: (Natural, Natural) -> (Natural, Natural)
f (m, n) = (m + 1, (m + 1) * n)
说明:
-
dot运算符
.实现 函数组合 的功能-
f (g x)===(f . g) x===f . g $ x -
f . g x===f . (g x)
-
斐波那契函数 (fold版本)
fib :: Natural -> Natural
fib = fst . (fold g (0, 1))
g :: (Natural, Natural) -> (Natural, Natural)
g (m, n) = (n, m + n)
05 序列相关的函数
Haskell 中的序列类型
对于任意类型 a,其对应的序列类型,可以书写为 [a]。
序列值的表示方式 (以[Natural]为例):
-
空序列:
[] -
包含一个自然数
1的序列:[1]或1 : []- 这里出现的单冒号
:是一个二元运算符
- 这里出现的单冒号
-
包含三个自然数
123的序列:[1, 2, 3]或1 : 2 : 3 : []- 可知:二元运算符
:满足右结合律
- 可知:二元运算符
序列上的 fold 函数
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr h c [] = c
foldr h c (x:xs) = h x (foldr h c xs)
foldl :: (b -> a -> b) -> b -> [a] -> b
foldl h c [] = c
foldl h c (x:xs) = foldl h (h c x) xs
序列上的若干函数
len :: [a] -> Natural
len [] = 0
len (n:ns) = 1 + len ns
| 原始递归版本 | fold函数版本 |
|---|---|
|
|
|
|
|
|
|
|
06 一种快速排序算法
qsort :: [Integer] -> [Integer]
qsort [] = []
qsort (n:ns) = (qsort $ filter (< n) ns) ++ [n] ++ (qsort $ filter (>= n) ns)
思考: 猜一猜,二元运算符
++的功能是什么?
Haskell还提供了一些语法机制,可以让qsort的定义更加结构化。
let ... in ... 表达式
qsort :: [Integer] -> [Integer]
qsort [] = []
qsort (n:ns) = let smaller = qsort $ filter (< n) ns
larger = qsort $ filter (>= n) ns
in smaller ++ [n] ++ larger
- 在
in后面的这个表达式中,可以访问let ... in之间定义的变量
where 子句
qsort :: [Integer] -> [Integer]
qsort [] = []
qsort (n:ns) = smaller ++ [n] ++ larger
where
smaller = qsort $ filter (< n) ns
larger = qsort $ filter (>= n) ns
let-in 表达式与where 子句的 区别:
在大部分情况下,两者没有本质的区别,仅仅反映了不同的表现形式
在一些情况下,
where 子句定义的变量具有更大的作用范围f x y | cond1 x y = g z | cond2 x y = h z | otherwise = k z where z = p x y
在
where 子句中定义的一个变量z,可在 guarded equations 的任何地方访问
let in 表达式不具有这样的能力
唐僧:
你的感觉如何?
我们用了一些朝三暮四的把戏 (规定一些语法规则),
把函数式思维的形式变得更容易理解了。小和尚:
我再观察一下;
如果你继续搞这些朝三暮四的小把戏,我就准备退课了!
Haskell 中标识符和运算符的命名规则
元素命名
在很多情况下,我们需要为程序中定义的元素 命名
-
所谓 “命名”,就是给一个东西赋予一个具有区分作用的名称
-
名称的作用:可以通过名称引用到所指向的那个程序元素
Haskell 中的名称,分为两大类:
-
标识符 (Identifier)
-
运算符 (Operator Symbol)
01 标识符的命名规则
-
由一或多个字符顺序构成
-
首字符只能是一个字母 (letter),具体包括:
- ASCII 编码表中的所有字母 (即:所有英文大小写字母)
- Unicode字符集中的所有字母
-
其他字符只能是
字母/数字/英文下划线/英文单引号 -
不能与 Haskell 的保留词重名
caseclassdatadefaultderivingdoelseforeignifimportininfixinfixlinfixrinstanceletmodulenewtypeofthentypewhere_
-
根据程序元素的不同,Haskell 还对标识符的首字符进行了进一步的限制
-
一些程序元素,其 标识符的首字符 只能是 大写字母
-
其他程序元素,其 标识符的首字符 只能是 小写字母
目前已经涉及到的程序元素包括:
-
函数 / 变量 / 类型变量:名称首字符必须是小写字母
-
类型:名称首字符必须是大写字母
-
-
02 运算符的命名规则
-
由一或多个符号 (symbol) 顺序构成,具体包括:
- ASCII 编码表中的所有符号:
!#$%&*+./<=>?@\^|-~: - Unicode 字符集中的大部分符号
- ASCII 编码表中的所有符号:
-
不能与Haskell的保留运算符重名
..:::=\|<-->@~=>
-
Haskell进一步将运算符分为两类:(1) 以英文冒号
:为首字符的运算符;(2) 其他运算符- 更多信息,按需说明
Hello, World!
01 Haskell 中的 Hello, World!
main = do
putStrLn "Hello, World!"
说明:
-
这是一个合法的 Haskell 程序 (符合 Haskell 语言规范)
-
它隐藏了一些代码,以至于看起来有些奇怪
-
恢复这些代码后,会得到一个更完整的程序:
module Main(main) where
import Prelude
main :: IO ()
main = do
putStrLn "Hello, World!"
-
module Main(main) where:- 这个文件定义了一个模块
Main - 这个模块对外输出了一个名称为
main的元素 - 这个模块中定义的元素出现在
where之后
- 这个文件定义了一个模块
Haskell 中的模块
关于模块 (Module),Haskell 语言规范中给出了如下信息:
一个 Haskell 程序由一或多个模块构成,且每一个模块定义在一个单独的文件中
一个 Haskell 程序必须包含一个名为
Main的模块
main元素的类型必须是IO t;其中,需要把t替换为一个具体的类型
IO是Prelude模块对外输出的一个元素,用于封装 IO 运算
Prelude模块对外输出的所有元素都会被默认加载到任何一个模块中一个 Haskell 程序的运行就是对
Main模块中的main元素进行求值的过程。
而且,最终获得的值会被抛弃。模块的名称必须满足如下两个条件之一
一个以大写字母开头的标识符。
- 例如:
MyModule两或多个以大写字母开头的标识符,通过字符
.连接在一起。
- 例如:
This.Is.Mymodule如果:一个模块在设计时就已经确定不会被其他模块所引用
那么:该模块可以放在任意一个具有合法名称的文件中
通常,
Main模块不会被其他模块所引用
因此,可以把Main模块放在任意一个文件中但是,将
Main模块所在文件名设定为Main,不失为一个好选择如果:一个模块可能会被其他模块所引用,
那么:该模块所在的文件必须满足如下条件:
如果:模块名是一个标识符,那么:模块所在文件的名称必须与模块名相同
如果:模块名是多个标识符通过
.字符连接在一起,那么:
模块所在文件的名称必须与模块名中最后的标识符相同
- 例如,模块
This.Is.Mymodule
必须放置在一个名为Mymodule的文件中
- 这里的文件名,不包含文件扩展名
模块名中前面的每一个标识符及其之间的顺序关系,
必须与文件系统的目录名以及目录之间的包含关系存在一一对应
- 例如,模块
This.Is.Mymodule
必须放置在源文件目录下的This/Is/Mymodule这个文件中。
-
import Prelude-
把
Prelude模块对外输出的所有程序元素加载到当前模块中 -
Haskell 规定:
-
若模块源码中不存在
import Prelude声明,则表明其缺省存在- 效果:你在程序中可以直接使用
Prelude输出的所有元素
- 效果:你在程序中可以直接使用
-
若模块源码中存在
import Prelude或其变体,则从Prelude中按需加载元素-
例如:如果模块中存在
import Prelude(Integer, (+), (-))
则表明只需把Prelude对外输出的类型Integer、加运算符、减运算符三个元素加载到当前模块中;Prelude对外输出的其他元素无需加载 -
例如:下面的 Haskell 模块定义不合法
module Main(main) where import Prelude(Integer, (+), (-)) main :: IO () main = do putStrLn "Hello, World!"原因:该模块中出现了两个未定义的元素
IOputStrLn
-
-
-
-
main :: IO ()-
main元素的类型是IO ()-
()是一个类型,称为0 元组(0-tuple) 类型 -
IO是一个类型构造器 (type constructor) -
IO ()是一个类型,其中封装了 IO 运算,且该运算会返回一个 0 元组
小和尚:
-
为什么
main的类型不是函数呢?C/C++/Java/Rust语言的main都是函数。
唐僧:
-
因为
main本来就不是函数。你在哪本数学书上见到过
main这样的函数?哪有函数一言不合就向控制台输出字符串的呢?
小和尚:
- 既然如此,C/C++等语言为什么把main作为函数呢?
唐僧:
-
我想,它们大概是为了让自己显得很 NB。
任何东西,能和数学沾上关系,就会显得高大上了
例如,有的公司举办了全球数学竞赛,又不公布成绩,...
-
-
-
main = do
putStrLn "Hello, World!"-
定义了
main中封装的 IO 运算 -
这个 IO 运算中仅包含了一个 IO action,即:在控制台输出一串字符
-
如果你愿意,可以继续添加一个IO action:
putStrLn "Hello, World! AGAIN"- 注意:应保持与上一行相同的缩进
小和尚:
do是什么梗?唐僧: 一言难尽啊!
- 简而言之:
do是一种语法糖 (syntax sugar)- 在函数的世界里,没有“顺序执行”这个概念 (这句话其实有些含糊)
- 但是,可以用一些机制去仿真“顺序执行”
do的作用就是把这些机制封装起来,让程序具有更好的易理解性
-
-
putStrLn "Hello, World!"-
putStrLn是Prelude模块输出的一个程序元素,定义如下:putStrLn :: String -> IO () putStrLn s = do putStr s putStr "\n"
-
02 一个具有更多交互性的程序
module Main(main) where
import Prelude
main :: IO()
main = do
putStrLn "Please input your name:"
name <- getLine
putStrLn $ "Hello, " ++ name
putStrLn "Please input an integer:"
str1 <- getLine
putStrLn "Please input another integer:"
str2 <- getLine
let int1 = (read str1 :: Integer)
let int2 = (read str2 :: Integer)
putStrLn $ str1 ++ " + " ++ str2 ++ " = " ++ (show $ int1 + int2)
-
name <- getLinegetLine是Prelude模块输出的一个元素,其定义如下:getLine :: IO String getLine = do c <- getChar if c == '\n' then return "" else do s <- getLine return (c:s)符号
<-是与do绑定的一种语法。在这行代码中,
<-的效果,暂时可以做如下理解:- 把
getLine返回的IO String类型的值中的那个String类型的值赋给name
- 把
-
let int1 = (read str1 :: Integer)这一行代码看来既熟悉又陌生:
- 我们看到了熟悉的
let,却没有看到它的好伙伴in - 这个
let就是let in中的let,用于定义在后面被使用的变量;
但是,in被语法糖隐藏了 (时机合适时,再介绍细节)
read str1 :: Integerread是Prelude输出的一个函数,其类型大约是String -> a- 这个表达式的效果:把一个字符串转换为一个整数值
- 在调用
read时,若无法从上下文中推断出a对应的具体类型,
则需在其后面放置:: X,显式说明a的具体类型为X
- 我们看到了熟悉的
-
show $ int1 + int2show是Prelude输出的一个函数,其类型大约是a -> Stringshow的功能:把一个值转换为一个字符串
唐僧:
- 掌握了Haskell 语言IO相关的操作,再加上前面介绍的知识,你应该可以做很多事情了
- 非常遗憾的是,这些程序目前还不能运行
- 不用太担心,想让程序运行,分分钟的事
小和尚:
- 分分钟是多久呢?
唐僧: 😅 ... (画外音:气氛突然有些尴尬)
Haskell程序的编译、运行、管理
当你用自然语言写了一本小说,可以把它发表在互联网上;
然后,读者们就可以阅读这本小说了当你用 Haskell 语言写了一个程序,也可以把它发表在互联网的某个代码托管网站上;
然后,程序员们就可以阅读这个程序了与小说不同的是,程序还有另外一类读者:计算机
- 计算机需要理解程序,并在各类硬件和软件资源的支持下,执行程序所表达的计算过程
对于程序设计语言的发明者们而言,定义语言的语法形式,仅仅是万里长征的第一步
为了让程序能够在硬件上运行,还需提供一系列软件支撑工具
这些工具又被称为程序设计语言的 工具链 (toolchain)
在本节中,我们主要介绍 Haskell 语言工具链中的三个基本工具:
-
GHC (Glasgow Haskell Compiler):
- 一种得到广泛使用的Haskell语言编译器,
能够把合法的Haskell程序变换计算机可执行的机器指令序列
- 一种得到广泛使用的Haskell语言编译器,
-
GHCi:
- Haskell程序的一种交互式 (interactive) 运行环境;
程序员可在其中输入任意合法的表达式,然后 GHCi 对表达式进行求值,并输出结果
- Haskell程序的一种交互式 (interactive) 运行环境;
-
Stack:
- 一种常用的 Haskell 软件项目构建管理工具
00 Haskell 工具链的安装
进入页面 https://www.haskell.org/ghcup/。
按照说明,在自己的计算机上安装 Haskell 工具链。
- 安装过程中总会遇到各种问题
- 遇到问题,莫慌张,主动寻求助教或其他同学的帮助
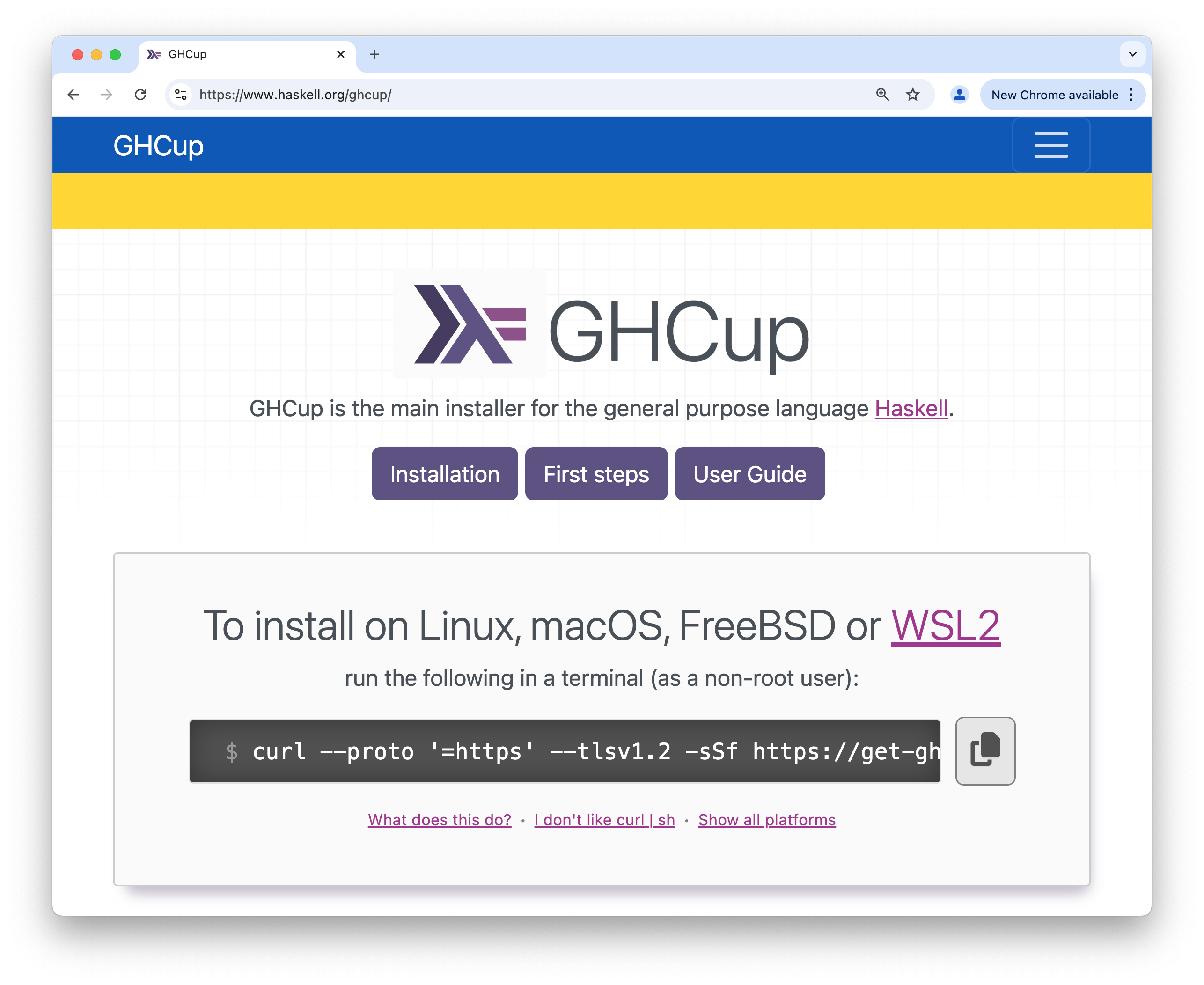
01 GHC 的使用
ghc 是 Haskell 语言的一种编译器 (compiler)
作用:把一个合法的 Haskell 程序转换/编译为在当前计算机上可运行的二进制程序
Step 1: 把下面的程序代码放置到某个文件夹下的Main.hs文件中
-- This is my first Haskell program
module Main(main) where
import Prelude
main :: IO ()
main = do
putStrLn "Hello, World!"
-
第一行为程序 注释 (comment)
- 注释就是对程序做的一些说明,不会改变程序的运行时行为
-
Haskell 的注释分为两类:
-
单行注释: 以两个连续连字符
--开始的一行文字 -
多行注释: 以
{-开始、以-}结束的所有文字
-
Step 2: 打开终端 (Terminal) 应用,把当前目录设置为Main.hs所在的文件夹
Step 3: 编译程序 (即:在终端中输入命令ghc Main.hs,并回车)
Step 4: 运行程序 (即:在终端中输入命令./Main,并回车)
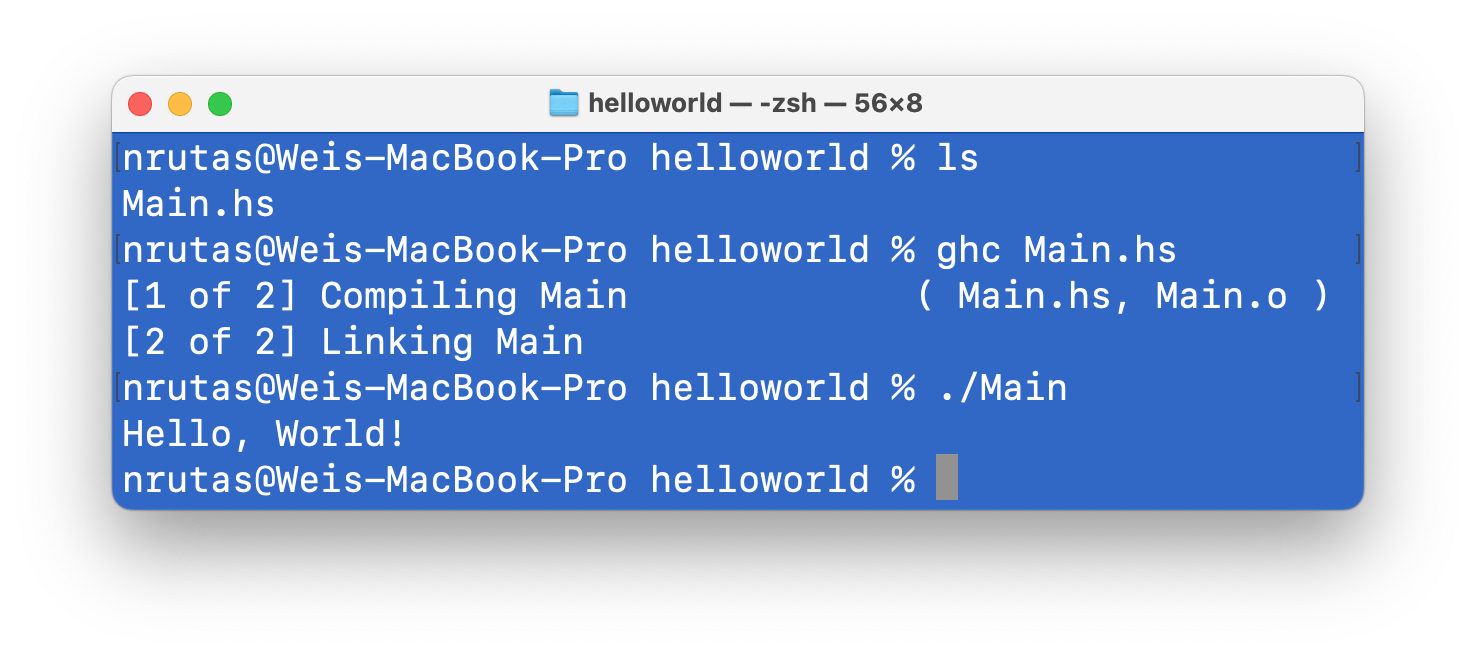
对于第一次接触程序设计语言的同学,这是一个具有历史意义的时刻。
这是人类的一大步,却只是个体的一小步。
许多年之后,面对未名湖边随风摇曳的垂柳,
你将会回想起,费尽千辛万苦终于成功运行这个无聊程序的那个遥远的夜晚。
动手练一练 01
请把前文介绍的那个更有交互性的 Haskell 程序,用 ghc 命令编译为可执行程序。
然后运行该程序,观察程序和你的交互过程。
关于 ghc 的详细使用说明,可访问其官方网站:https://www.haskell.org/ghc/
- 没事不要打开这个链接;打开了也看不懂。
你需要在学习过编译原理相关的知识后,再来看一看。
02 GHCi 的使用
ghci 是 Haskell 程序的一种交互式运行环境。
ghci 默认加载Prelude模块;因此,可直接使用该模块输出的元素
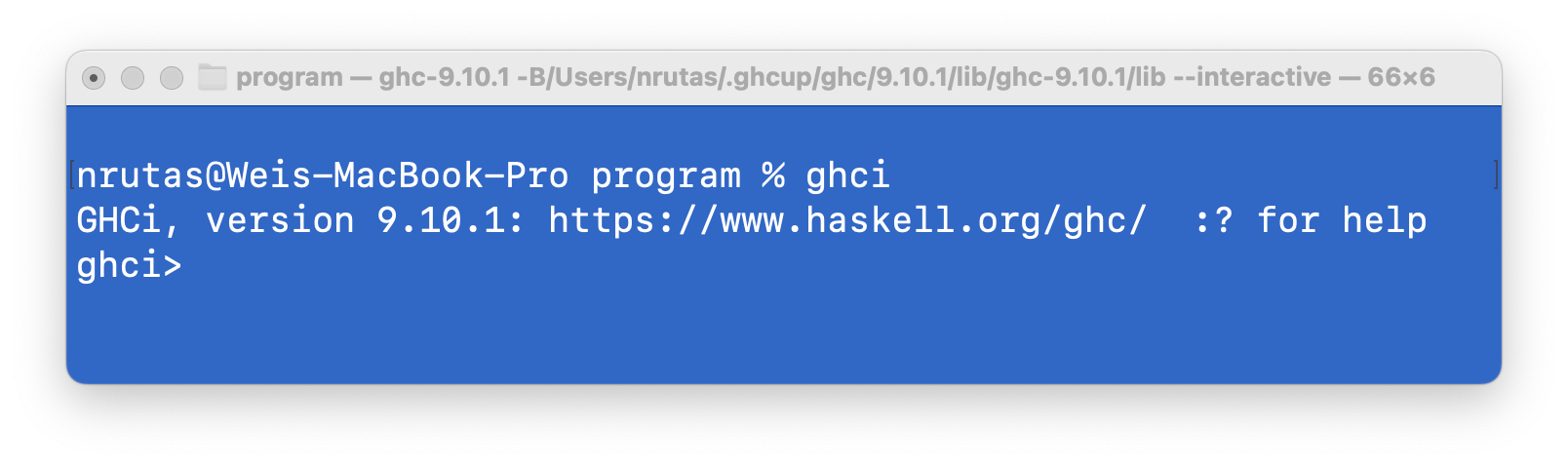
你可以在其中输出合法的 Haskell 表达式;ghci 会输出求值结果。
ghci 中的常用命令:
-
:?列出ghci支持的所有命令 -
:quit或:q退出当前ghci环境 -
:load <模块文件名>把一个指定的模块加载到当前环境中 -
:reload重新加载那些已经加载的模块 (这些模块可能被修改了)
:load命令使用示例:
- 打开终端 (Terminal) 应用,把当前目录设置为
Main.hs所在的文件夹
动手练一练 02
- 把前文介绍的快速排序函数
qsort封装在一个 Haskell 模块中;- 在 ghci 中加载这个模块;
- 在 ghci 中对
qsort函数的正确性进行测试
- 即:把这个函数作用到若干序列数据上,观察函数的返回值是否符合预期
03 Stack 的使用
stack 是一种面向 Haskell 程序开发的构建管理工具。
其管理内容覆盖:代码组织方式、编译器版本及编译参数、外部依赖关系、测试等。
ghc、ghci 适合做一些小打小闹的事情:
- 例如,学习 Haskell 语言、编写一个小规模的 Haskell 程序等
- 其中,ghci 可以作为一种入门级的程序调试环境
真实的软件开发是一种面向群体的智力密集型活动。
小和尚:
- 我就一个人开发一个复杂的软件应用,不可以吗?
唐僧:
可以,一个建筑工人也可以独立建造一栋摩天大楼;只要给他足够的时间。
群体软件开发还面临各种复杂的管理问题
- 包括:人力资源管理、需求管理、软件制品管理、编译环境管理、开发进度管理等
工欲善其事,必先利其器:需要采用合适的工具应对这些问题
下面,我们基于stack 的官方使用说明,对它进行简要的介绍。
stack new 命令
-
使用
stack new命令,可以创建一个具有特定名称的软件开发项目,其中包含一个包(package) -
Package这个概念在语言规范中并不存在,但在实践中得到广泛应用。
在逻辑上,一个 package 包含若干相关的 Haskell 模块。
- 例如:可以把一个完整的Haskell程序打包为一个package,其中包含一个Main模块、若干个被Main模块加载的自定义模块、以及相关的测试模块。
-
一个 package 具有一个全局唯一的名称
- package 的名称由若干个单词通过连字符
-连结在一起 - 每个单词由若干字母或数字组成,且至少包含一个字母
- package 的名称由若干个单词通过连字符
如果要在一个特定的文件夹下创建一个名称为foo的项目,可以这么做:
-
打开终端应用,将当前目录设定为项目所在的文件夹
-
运行如下命令 (确保你的计算机处于联网状态)
stack new foo
如果一切顺利,当前文件夹下会存在一个名为foo的文件夹
foo项目的所有信息都被放在这个文件夹中
使用cd foo命令进入这个文件夹,可以看到其中存在的信息:
. ├── CHANGELOG.md ├── LICENSE ├── README.md ├── Setup.hs ├── app │ └── Main.hs ├── foo.cabal ├── package.yaml ├── src │ └── Lib.hs ├── stack.yaml ├── stack.yaml.lock └── test └── Spec.hs
stack build 命令
- 在终端的
foo目录下输入命令stack build对foo项目进行构建
stack exec 命令
-
在终端的
foo目录下输入命令stack exec foo-exe,运行当前项目- 如果你觉得
foo-exe这个名字不好,可以在配置文件中修改成另外一个
- 如果你觉得
stack test 命令
-
在终端的
foo目录下输入命令stack test,可以触发对当前项目的测试-
stack 已经帮助我们建立了一个空的测试程序
-
我们需要根据项目的实际内容向其中填写相应的测试代码
-
例如,如果你自己编写了一个排序函数,为了确保功能的正确性,你需要在若干种具有代表性的数据上测试排序函数的输出是否符合你的预期。
-
只要把这些测试数据按照规定的方式写在特定的文件中,
stack test命令就会自动执行对应的测试活动,并给出测试结果.
-
-
stack 在foo项目中创建的文件
-
三个文件:
LICENSE/README.md/CHANGELOG.md-
LICENSE声明当前项目版权相关的信息 -
README.md对当前项目的简要说明、 -
CHANGELOG.md记录项目在不同版本中发生的变更情况
- 这三个文件不会参与到编译活动中,不会对构建过程产生影响
-
-
两个文件:
helloworld.cabal/Setup.hs- 这是更底层的构建工具
cabal相关的两个文件;无需关注
- 这是更底层的构建工具
-
一个文件:
stack.yaml。其中记录了两条信息:packages: - .- 含义:当前项目中包含一个 package,它就存在于
stack.yaml所在的文件夹中
snapshot: url: https://raw.githubusercontent.com/commercialhaskell/stackage-snapshots/master/lts/24/4.yaml- 含义:一个 URL,指向互联网上的一个 yaml 文件,其中指明了当前项目使用的 GHC 版本以及一些可用的外部 package
- 含义:当前项目中包含一个 package,它就存在于
-
一个文件:
package.yamlname: foo version: 0.1.0.0 github: "githubuser/foo" license: BSD-3-Clause author: "Author name here" maintainer: "example@example.com" copyright: "2025 Author name here" extra-source-files: - README.md - CHANGELOG.md # Metadata used when publishing your package # synopsis: Short description of your package # category: Web # To avoid duplicated efforts in documentation and dealing with the # complications of embedding Haddock markup inside cabal files, it is # common to point users to the README.md file. description: Please see the README on GitHub at <https://github.com/githubuser/foo#readme> dependencies: - base >= 4.7 && < 5 ghc-options: - -Wall - -Wcompat - -Widentities - -Wincomplete-record-updates - -Wincomplete-uni-patterns - -Wmissing-export-lists - -Wmissing-home-modules - -Wpartial-fields - -Wredundant-constraints library: source-dirs: src # 当前项目的 lib 文件放在 src 文件夹中 executables: foo-exe: # stack exec 命令后跟的那个名字;可以被修改为其他名称 main: Main.hs # main 元素定义在 Main.hs 中 source-dirs: app # foo-exe 的源文件放在 app 文件夹中 ghc-options: - -threaded - -rtsopts - -with-rtsopts=-N dependencies: - foo tests: foo-test: main: Spec.hs source-dirs: test ghc-options: - -threaded - -rtsopts - -with-rtsopts=-N dependencies: - foo -
三个 hs 文件:
-
app/Main.hsmodule Main (main) where import Lib main :: IO () main = someFunc -
src/Lib.hsmodule Lib ( someFunc ) where someFunc :: IO () someFunc = putStrLn "someFunc" -
test/Spec.hsmain :: IO () main = putStrLn "Test suite not yet implemented"
-
唐僧: 我想,你大概明白
stack new foo做了什么吧?
它帮我们创建了一个 Haskell 程序的骨架以及编译和运行环境。
- 所有的这一切,stack 都进行了很好的封装,使得我们只需要使用stack提供的几个命令,就能对一个软件开发项目进行便捷的管理
动手练一练 03
请使用stack 创建一个名为qsort 的项目。然后:
- 在
src/Lib.hs中添加并输出前面介绍的qsort函数;- 在
app/Main.hs中加载Lib模块,
然后,找几个待排序的数据,用qsort函数对它们进行排序,打印出排序的结果
基于 stack 的 package 管理
-
有人说,他站在了巨人的肩膀上,看到了很远的地方
此言确实不虚,在软件开发中也是如此
-
在真实的软件开发项目中,很少有开发者从零开始编写所有的软件代码
开发者总是尽可能复用其他开发者已经开发完成的功能模块。
- 例如,前面我们看到的
Prelude模块就是 Haskell 标准库提供的一个模块。 - Haskell 标准库还提供了很多其他模块;具体参见Haskell语言规范
- Haskell 也提供了 import 语句来支持对其他模块的复用
- 例如,前面我们看到的
-
但是,事情并没有到此结束
-
软件开发者群体是一个乐于分享的群体
-
有很多程序员耗费了大量的精力,开发出很多高质量的软件模块,然后把这些模块放在互联网,供其他开发者免费使用
-
然后,其他开发者在前人开发的模块的基础上又开发出新的模块,并共享到开发者群体中
-
长此以往,就形成了一种欣欣向荣的生态系统
-
在这个生态系统中,丰富多样的软件模块不断涌现,持续演化,就像自然界生态系统所展现出的物种的多样性和持续演化那样
-
-
这种乐于分享的特点在 Haskell 开发者群体中也是存在的,也在此基础上形成了欣欣向荣的生态
-
在这个生态系统中,开发者分享工作成果的基本单位是 package,
- 也即:一个开发者把一组相关的Haskell模块封装为一个package,然后将其发布到互联网上
小和尚:
- 分享工作成果的基本单位什么不能是模块呢?
唐僧:
其实,你把一个模块单独封装为一个package也是可以的
在更一般的意义上,不以模块作基本发布单位的主要原因如下:
模块不存在版本的概念
- 在软件开发生态系统中,演化是一种常态
- 缺失了版本的概念,使得我们不能对同一个模块的不同版本进行有效管理
在很多场景下,模块过于细粒度
- 如果要对外发布一个复杂的Haskell应用程序,以模块为基本单元显然不合适
当你对外发布一个模块时,为了使得其他开发者对该模块的质量具有足够的信心,你可能还需要将该模块的测试数据和程序一起对外发布。此时,将一个模块以及附带的测试模块打包一个 package,具合理性.
-
使用
stack new创建的项目,其中就包含了一或多个 package- 这些 package 的信息记录在
stack.yaml文件的packages配置项中 - 例如,在
foo项目中,packages 下面只包含一个值,即:点符号.- 这表明,在
foo项目的根目录中存在一个 package
- 这表明,在
- 这些 package 的信息记录在
-
在 stack 项目中,每一个 package 的管理信息记录在一个名为
package.yaml的文件中.-
该文件包含一个重要的配置项
dependencies-
它记录了当前 package 依赖的所有其他 package 的名称与版本信息
-
例如,在
foo项目包含的唯一一个 package 的package.yaml文件中,配置项dependencies信息如下:dependencies: - base >= 4.7 && < 5- 含义:当前 package 依赖于一个名称为
base的 package,且要求base的版本号落在区间[4.7, 5)中
一个重要问题:如何获得这个名称为base的特定版本的 package 呢?
- 含义:当前 package 依赖于一个名称为
-
-
-
Haskell 社区维护了一个在线的 package 仓库,并将其命名为 Hackage
https://hackage.haskell.org/任何一个开发者都可以向这个仓库中发布自己开发的 package,也可以从这个仓库中下载特定名称和特定版本的 package
-
你可以在 Hackage 中搜索名称为
base的 package在结果页面上,可以看到
base的所有版本,和每一版本包含的所有模块在长长的模块列表中,会看到两个熟悉的名字:
Prelude和Numeric.Natural- 因为
base包含了这两个模块,且当前的项目依赖于base,所以,在当前项目中,就可以使用import语句加载这两个模块了
- 因为
-
你可以在
package.yaml文件的dependencies配置项中添加更多的 package 名称以及对应的版本需求然后,使用
stack build命令,stack 就会自动到 Hackage 仓库中下载对应 package如果你不相信,就试试下面的练习吧
动手练一练 04
Hackage 中有一个名称为
random的 package:
- 其中包含一个名称为
system.Random的模块;其中定义了一个名称randomIO的元素。在 do 后面的代码块中,使用
rnd <- randomIO :: IO Int,就能得到一个随机生成的整数。请完成如下事情:
使用 stack 创建一个名称为
random-num的项目在 package.yaml 文件的
dependencies下添加一个值:random == 1.2.0
- 含义:当前 package 依赖一个名称
random、版本1.2.0的 package- 在Mac的M系列芯片上,可能需要把这个值修改为
random >= 1.2 && < 2在当前项目中实现 “向终端打印出一个随机数” 的功能
请特别注意,当你使用
stack new命令后,终端的输出信息。
-
需要指出的是,在主流的程序设计语言开发社区中,都存在类似的package管理方式
-
即:一个被开发者广泛认同的 package 仓库、一个配套的构建管理工具。
- 这是在互联网时代形成的一种群体软件开发模式,可能会陪伴你很长的时间。
- 选择一个开发者社区,选择一个有价值的软件开发项目,努力成为项目的核心贡献者,你会收获很多很多。
-
-
关于 stack,暂且讲到这里吧。有兴趣的同学可自行阅读相关材料
Haskell 程序的书写
Haskell 程序的 “书写风格”
对于学习过C / C++ / Java语言的同学而言,可能会觉得Haskell程序的书写有些奇怪
-
在传统语言中,源程序中会出现大量的分号
;和花括号对{ ... }- 前者的作用:作为一条语句的终结符
- 后者的作用:把几条语句封装为一个代码块 (Code Block)
-
但是,在前面出现的 Haskell 程序中,从来没有看到过花括号和分号。
其实,你误解 Haskell 了。
-
Haskell 规定,在
where/let/do/of这四个关键词后,需要放置一个代码块 -
在代码块的书写上,Haskell提供了两种书写风格:
-
Layout-sensitive (排布无关)
- 利用代码行的缩进表示语句的结束或代码块的结束
-
Layout-insensitive (排布相关)
- 利用分号表示语句的结束,利用一对花括号形成一个代码块
-
-
下面是前文出现的一个采用 layout-sensitive 风格书写的源程序
module Main(main) where import Prelude main :: IO() main = do putStrLn "Please input your name:" name <- getLine putStrLn $ "Hello, " ++ name putStrLn "Please input an integer:" str1 <- getLine putStrLn "Please input another integer:" str2 <- getLine let int1 = (read str1 :: Integer) let int2 = (read str2 :: Integer) putStrLn $ str1 ++ " + " ++ str2 ++ " = " ++ (show $ int1 + int2)对应的 layout-insensitive 程序如下:
module Main(main) where { import Prelude; main :: IO(); main = do { putStrLn "Please input your name:"; name <- getLine; putStrLn $ "Hello, " ++ name; putStrLn "Please input an integer:"; str1 <- getLine; putStrLn "Please input another integer:"; str2 <- getLine; let { int1 = (read str1 :: Integer); }; let { int2 = (read str2 :: Integer); }; putStrLn $ str1 ++ " + " ++ str2 ++ " = " ++ (show $ int1 + int2); } }唐僧:
- 你更喜欢哪一种风格呢?
- 由繁入简易,由简返繁难;回不去咯!
小和尚:
- 在采用 layout-sensitive 风格书写程序时,如何确定一行代码的缩进长度?
唐僧: 记住三条朦胧的准则:
-
相同缩进 => 开始一条新语句
-
更多缩进 => 继续上一条语句
-
更少缩进 => 结束一个代码块
Haskell 程序的 “书写方式”
Haskell 提供了两种源程序的书写方式:
-
文件扩展名为
hs的书写方式把 layout-insensitive/sensitive 风格的程序放置在扩展名为
hs的文件中 -
文件扩展名为
lhs的书写方式注释 与 其他代码 的地位发生了变化:
- 书写注释时,不需要使用 前缀
--或起始/终止字符串{-/-}; - 书写其他代码时,每一行开始必须添加 符号
>
- 书写注释时,不需要使用 前缀
| hs | lhs |
|---|---|
|
|
-
注意:lhs 文件的书写存在一个硬性的要求
- 以符号
>开始的代码行 与 注释 之间 至少存在一个空行
- 以符号
小和尚:
- 为什么要发明lhs这种书写方式呢?
唐僧:
- 这个问题,你自己慢慢体会吧;不重要。
本章作业
作业 01
关于逻辑与 (and) 函数,你还能想到其他定义方式吗?
请用 Haskell 语言写出至少其他三种定义方式。
作业 02
请用目前介绍的 Haskell 语言知识,给出函数
div的一种或多种定义。
- div :: Integer -> Integer -> Integer
说明:
- 不用关注效率
- 不用关注第二个参数为 0 的情况
- 如果你认为这个问题无解或很难,请给出必要的说明
- 为什么无解? 或者,困难在哪里?
作业 03
关于阶乘函数,你还能想到其他定义方式吗?
请分别使用 “guarded equations” 和 “conditional expression” 写出阶乘函数的定义。
作业 04
小明同学学习了这么多 Haskell 语言的知识后,感觉很累。
于是,他想用 Haskell 语言编写一个简单的命令行游戏让自己放松一下。这个游戏描述如下:
- 系统随机生成一个 1~100 之间的整数,记为
x- 在命令行中提示用户输入一个整数
- 接收用户输入的整数,记为
x’- 如果
x’ < x,提示用户他/她输入的值比真实值小,跳转到2- 如果
x’ > x,提示用户他/她输入的值比真实值大,跳转到2- 如果
x’ == x,提示用户他/她成功了,游戏结束小明同学太累了,所以想请你帮他写一个这样的程序。你觉得这个事情可行吗?
- 请尝试编写一个这样的程序
- 如果你发现这个事情有困难,请告诉我们:
- 你的求解思路是什么 (多种思路也可以) ?
- 在按照一个思路前进的过程中,遇到了什么困难,使得你无法继续走下去
第 04 章:类型与类簇
中英文对照:
- 类型 =>
Type- 类簇 =>
Type Class
小和尚:
- 为什么不把 “Type Class” 翻译为 “类型类” 呢?
唐僧:
- 这是一件鸡毛蒜皮的事情;甚至后面很多地方使用的就是 “类型类”
- 最好的应对方式:不做任何翻译,直接用原始的英文
01 类型
类型是什么
在 Haskell 中,
-
一个类型是由一组值构成的集合
-
例如,
Bool类型,包含两个值:TrueFalse
类型错误 (Type Error)
当在应用一个函数时
- 如果:“传入的实际参数” 的类型 与 “函数的形式参数” 的类型 不一致,
- 则称:发生了 类型错误
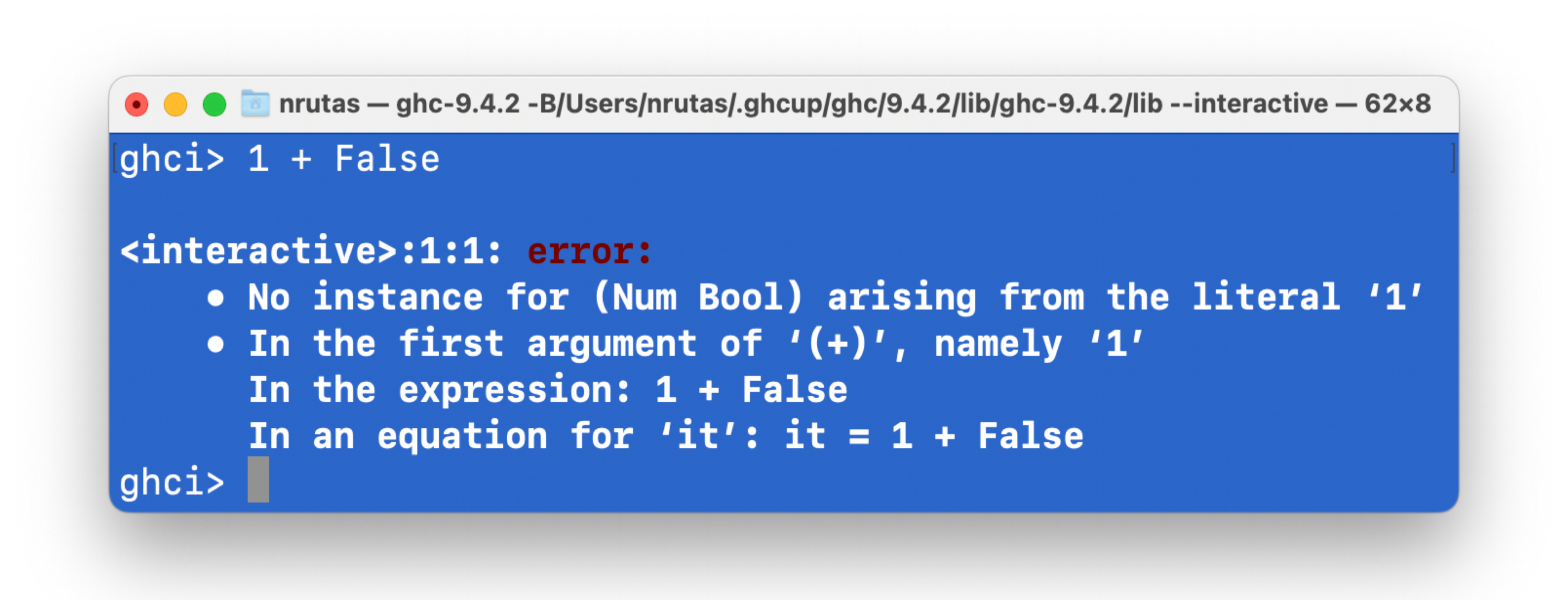
-
在上面这个示例中,
-
+运算符接收的两个参数应该都是数值 -
实际传给
+运算符的第二个参数False不是一个数值,而是Bool类型的一个值 -
因此,产生了类型错误
-
表达式的类型
如果一个表达式 e 在评估后会得到类型 T 的一个值,则称:e 的类型为 T
- 在 Haskell 程序中写作:
e :: T
任何一个良构的表达式 (Well-formed Expression) 都具有一个确定的类型
-
表达式的类型在编译时刻即能够自动被确定
-
确定表达式的类型的过程,称为 类型推导 (Type Inference)
f :: A -> B, e :: A -----------------------[app] f e :: B上面是类型论中非常经典的一条推导规则;含义如下:
-
如果:表达式
f的类型为A -> B,且 表达式e的类型为A -
那么:表达式
f e的类型为B
-
-
所有的类型错误在编译时刻都会被发现
- 因此,无需在运行时刻进行类型错误的检查,从而提高了程序运行的安全型和效率
在 GHCi 中,使用命令 :type 可以确定一个表达式的类型 (无需评估这个表达式的值)
02 Haskell 中的基础数据类型
Bool
该类型具有两个逻辑值:True False
- exported by Prelude (即:该类型是
Prelude模块的输出元素之一)
前面已经介绍:
Prelude输出的所有元素都会被自动导入到任何模块中
- 因此,在程序中可以直接使用
Prelude输出的元素
Char
该类型的每一个值,对应 Unicode 字符编码规范中的一个字符 (code point)
-
关于 Unicode 字符的更多信息请参看 http://www.unicode.org/
-
exported by Prelude
String
该类型在 Haskll 中的定义:type String = [Char]
-
即,一个字符串是一个由
Char类型的值形成的List -
exported by Prelude
Int
一种定长的整数类型
-
在 GHC 编译器中,该类型能够表达的整数范围是
[-2^63, 2^63 - 1] -
exported by Prelude
Integer
一种不定长的整数类型
-
因此,可以表达任何一个整数值
-
exported by Prelude
Word
一种定长的无符号整数类型
-
与
Int具有相同的长度 -
exported by Prelude
Natural
一种不定长的无符号整数类型
-
因此,可以表达任何一个自然数
-
exported by
Numeric.Naturalin thebasepackage
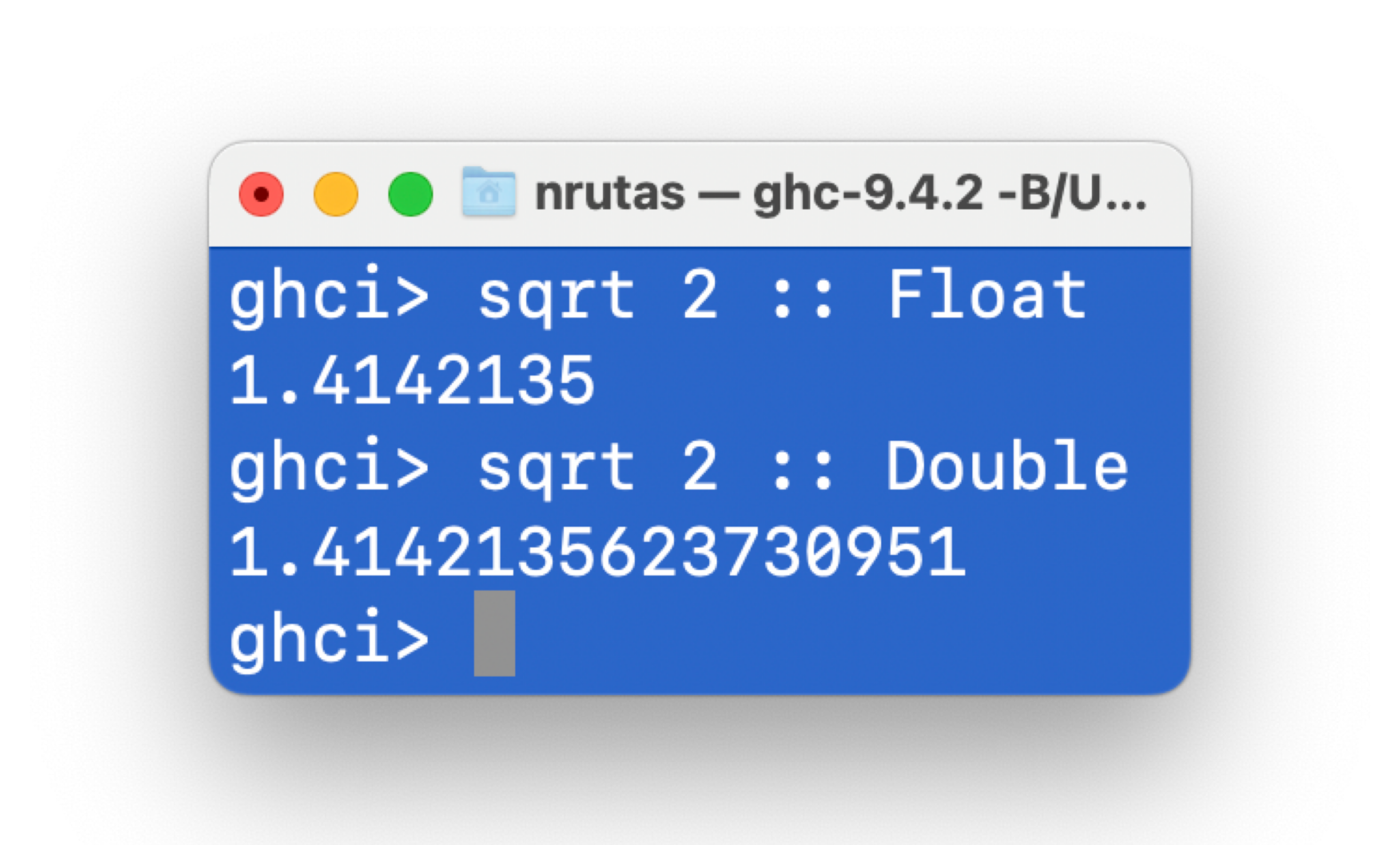
Float / Double
单/双精度浮点数类型 (exported by Prelude)
03 List 类型
一个 list 是由若干个相同类型的值形成的序列。
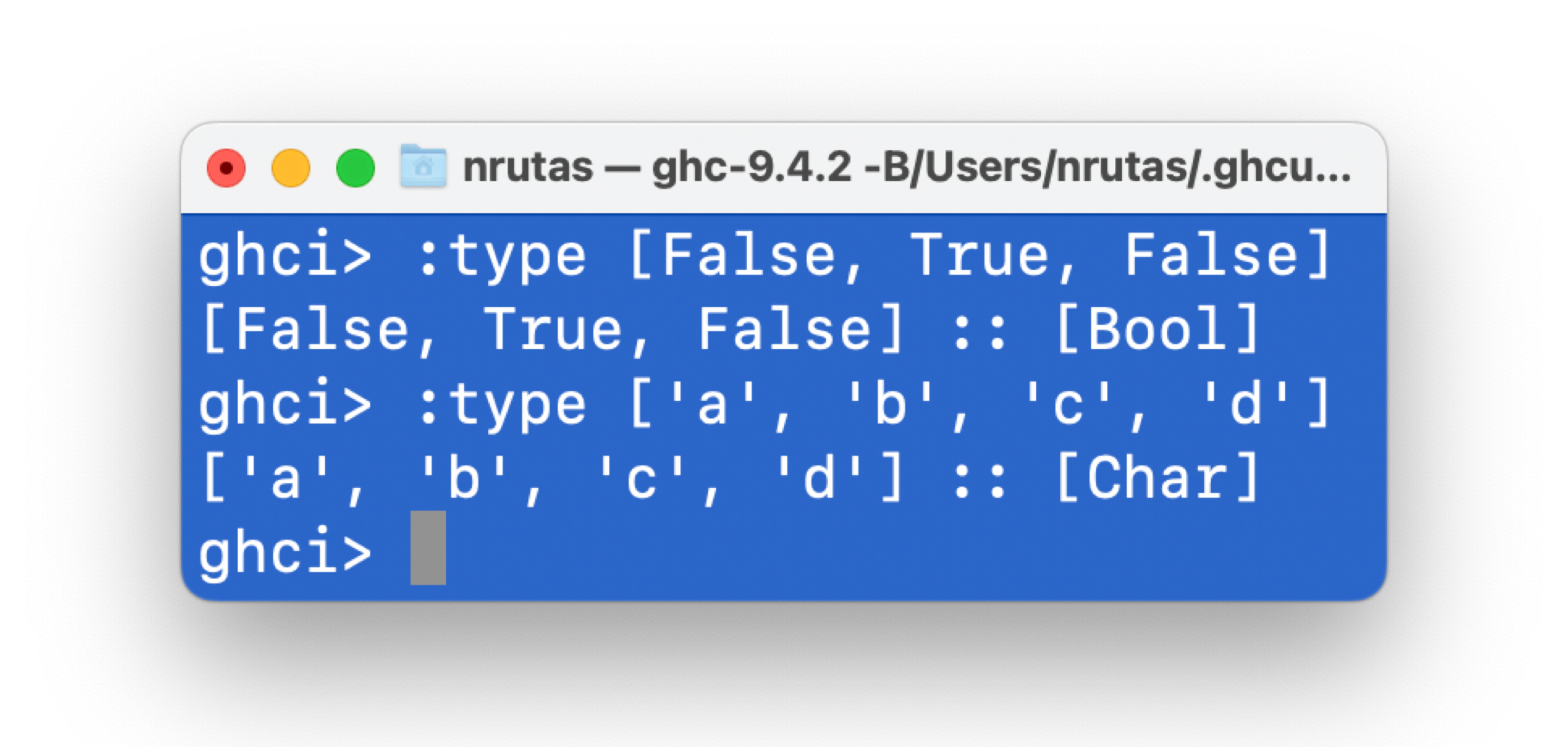
给定一个类型 T,[T]是一个类型
[T]的每一个值,都是一个元素类型为T的 list
重要信息:
-
[T]类型没有对 list 的长度信息 (即,list 中元素的数量) 进行任何限制- 因此,包含
1个T元素的 list、包含0个T元素的 list、以及包含3个T元素的 list,它们的类型都是[T]
- 因此,包含
-
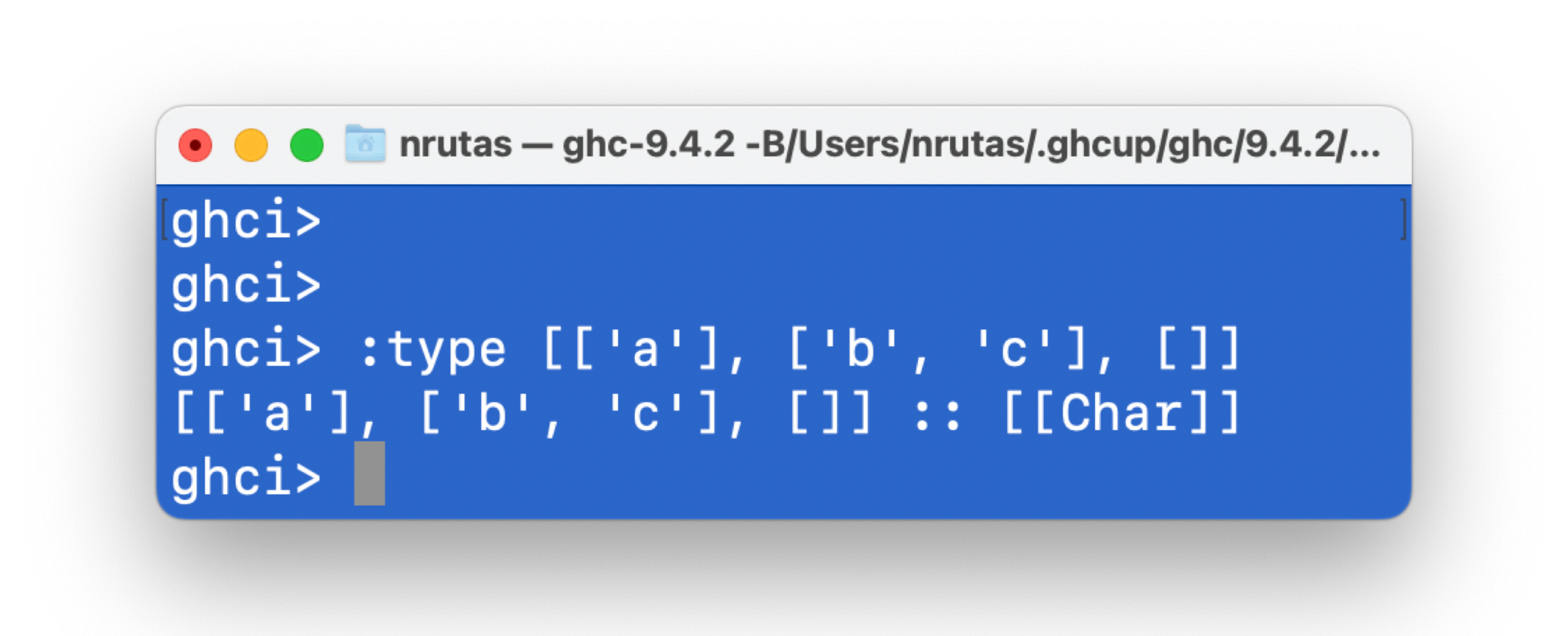
任何一个类型
T,都具有一个对应的[T]类型- 因此,
[[T]]也是一个合法的类型
- 因此,
04 Tuple 类型
给定两个类型 X 和 Y:
-
(X, Y)是一个二元组 (2-tuple) 类型-
该类型的任何一个值具有形式
(x, y),满足:x :: X且y :: Y -
在集合论中,类型
(X, Y)就是两个集合X和Y的笛卡尔积
-
给定三个类型 X Y Z:
-
(X, Y, Z)是一个三元组 (3-tuple) 类型- 该类型的任何一个值具有形式
(x, y, z),满足:x :: X、y :: Y且z :: Y
- 该类型的任何一个值具有形式
类似地,还有 4-tuple、5-tuple、...
重要信息:
-
Haskell 中 不存在 一元组 (1-tuple) 类型
-
Haskell 中 存在 零元组 (0-tuple) 类型
-
零元组类型,写作
() -
零元组类型具有唯一一个值,写作
()
小和尚:
- 零元组类型 和 唯一的零元组值 在形式上都是
();这不会产生混乱吗?
唐僧:
-
你的观察很仔细,非常棒 👍
-
不用担心,在 Haskell 中,类型和值具有截然不同的上下文
- 因此,从
()的上下文能够判定 “它到底是类型还是值”
- 因此,从
-
-
三元组和更多元组,在理论上,没有存在的必要 (在实践中,为了使用上的方便,有存在的必要)
-
原因:基于二元组,可以构造出三元组、四元组、...
-
例如:
(1, (2, 3))是一个采用二元组表示的三元组
-
05 Function 类型
给定两个类型 X 和 Y:
-
X -> Y是一个函数类型- 该类型的每一个值都是一个函数,且该函数把类型
X的值映射到类型Y的值
- 该类型的每一个值都是一个函数,且该函数把类型
重要信息:
-
任何类型都可以作为类型
X -> Y中的X和Y例如:List 类型 和 Tuple 类型都可以作为
X和Yadd :: (Int, Int) -> Int add (x, y) = x + yzeroto :: Int -> [Int] zeroto n = [0..n] -- 这里有一个细节的语法 -- [0..n] 表示一个 list,其中依次包含从 0 到 n 的所有整数值
05.01 柯里化函数 (Curried functions)
小和尚:
- “柯里化” (Curried) 这个奇怪的名字来源于哪里呢?
唐僧:
- 如果这么说,那么 “Haskell” 这个奇怪的名字又来源于哪里呢?
希望很多年以后,你的 “姓” 或 “名” 也能出现在教科书中。
给定一个函数 f :: A -> B
-
如果:
A是一个二元组类型, -
那么:我们可以通过柯里化,把
f转换为一个等价的但第一个参数不再是元组类型的函数 -
例如,上面出现的函数
add :: (Int, Int) -> Int,它对应的柯里化函数为:add :: Int -> Int -> Int add x y = x + y
类似地,如果函数的第一个参数是n元组类型,我们也可以通过柯里化把第一个参数拆解开。例如:
mult :: (Int, Int, Int) -> Int
-- 柯里化版本
mult :: Int -> Int -> Int -> Int
Haskell 的 Prelude 模块中定义了两个函数:
curry :: ((a, b) -> c) -> a -> b -> c
curry f x y = f (x, y)
uncurry :: (a -> b -> c) -> ((a, b) -> c)
uncurry f p = f (fst p) (snd p)
-
这两个函数支持在 “非柯里化函数” 和 “柯里化函数” 之间相互转换
- 把类型中出现的
abc,理解为任意类型即可
- 把类型中出现的
与非柯里化函数相比,柯里化函数具有更好的灵活性:
-
应用 非柯里化函数 时,需要一次提供全部的参数
-
应用 柯里化函数 时,可以按需传入参数
-
例如,对于上面引入的
mult函数,如下应用方式都是合法的:mult 2,mult 2 3,mult 2 3 4
-
关于柯里化函数的一个语法约定 (Conversion)
-
运算符
->满足右结合律- 例如:
Int -> Int -> Int -> Int等价于Int -> (Int -> (Int -> Int))
- 例如:
06 多态函数 (Polymorphic Functions)
称一个函数为 多态函数,
- 如果它的类型中包含一或多个 类型变量 (type variable)
例如,如下是一个多态函数:
len :: [a] -> Natural
len [] = 0
len (n:ns) = 1 + len ns
-
在 Haskell 中,类型声明中 “以小写字符开头” 的标识符,被编译器视为一个 类型变量
-
len的类型的含义:- 对于任意类型
a,len函数接收一个[a]类型的值,返回一个自然数
- 对于任意类型
-
在实际应用
len函数的时候,编译器会根据传入的参数的类型,推导出a的具体类型
Prelude 模块中的若干多态函数
fst :: (a, b) -> a
fst (x, _) = x
- 获得二元组中第一个分量
snd :: (a, b) -> b
snd (_, y) = y
- 获得二元组中第二个分量
head :: [a] -> a
head (x:_) = x
-
获得一个 list 中的第一个元素
-
注意:
head是一个 partial function,因为它在 “长度为零的 list” 上没有定义
tail :: [a] -> [a]
tail (_:xs) = xs
- 获得一个 list 中删除第一个元素后的 list;仍然是一个 partial function
last :: [a] -> a
last [x] = x
last (_:xs) = last xs
- 获得一个 list 中的最后一个元素;仍然是一个 partial function
重载函数 (Overloaded Functions)
称一个多态函数为 重载函数
- 如果它的类型中包含一或多个 类型类约束 (type class constraint)
例如,如果你在 ghci 中输入命令 :type (+),就会看到 (+) 的类型
ghci> :type (+)
(+) :: Num a => a -> a -> a
-
在这个类型中,
=>左侧的东西,称为 类型类约束 -
这个约束的含义是:适用于
(+)的类型a必须是类型类Num的一个实例
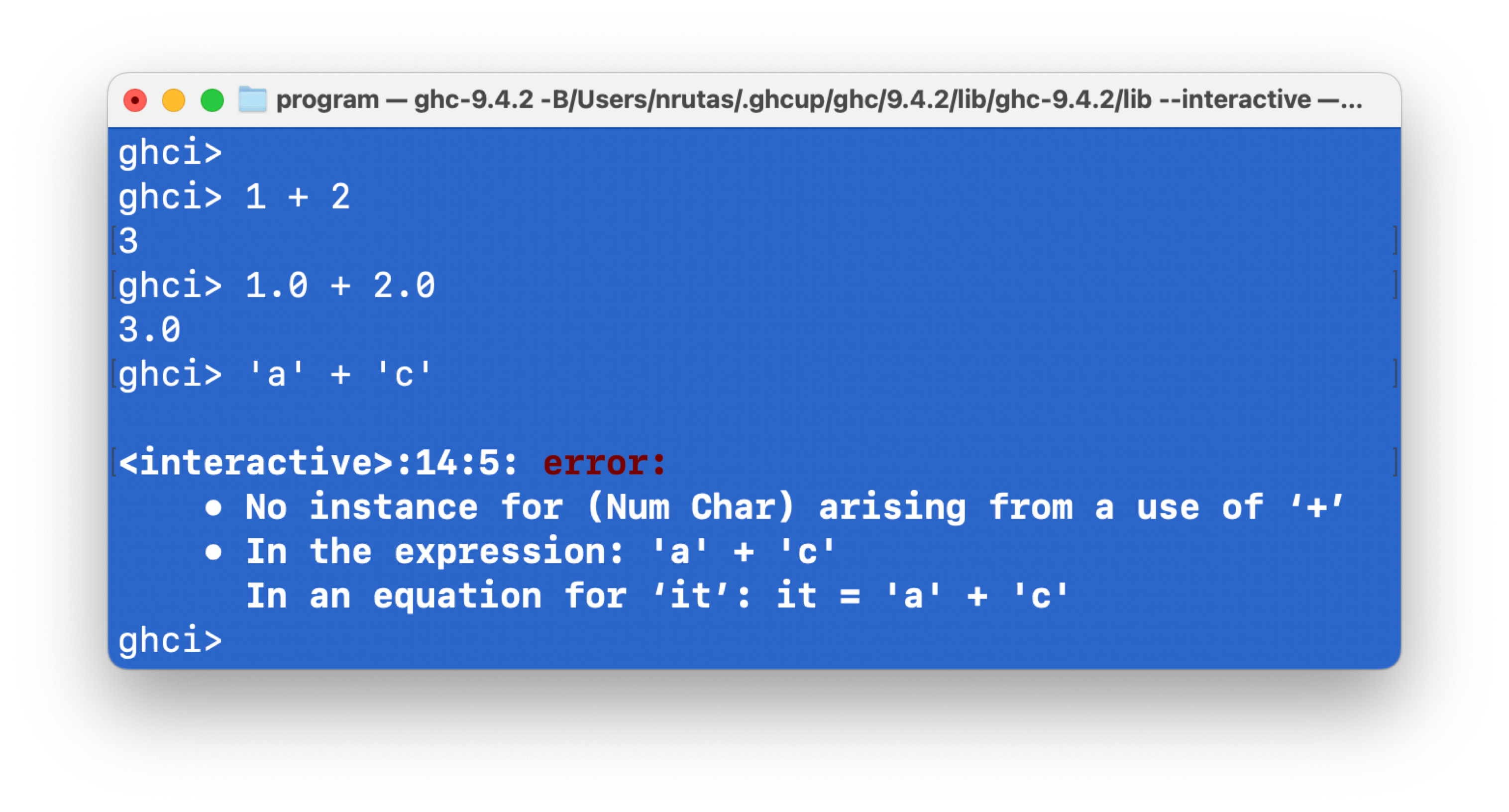
上面这个截图表明:
-
(+)适用于 “整数” 和 “浮点数”,但是不适用于 “字符” -
原因:类型
Char不是类型类Num的实例
07 类型类 (Type Class)
Prelude 模块输出了很多类型类,其中最基础的三个是:
EqOrdNum
这三个类型类出现在了很多函数中:
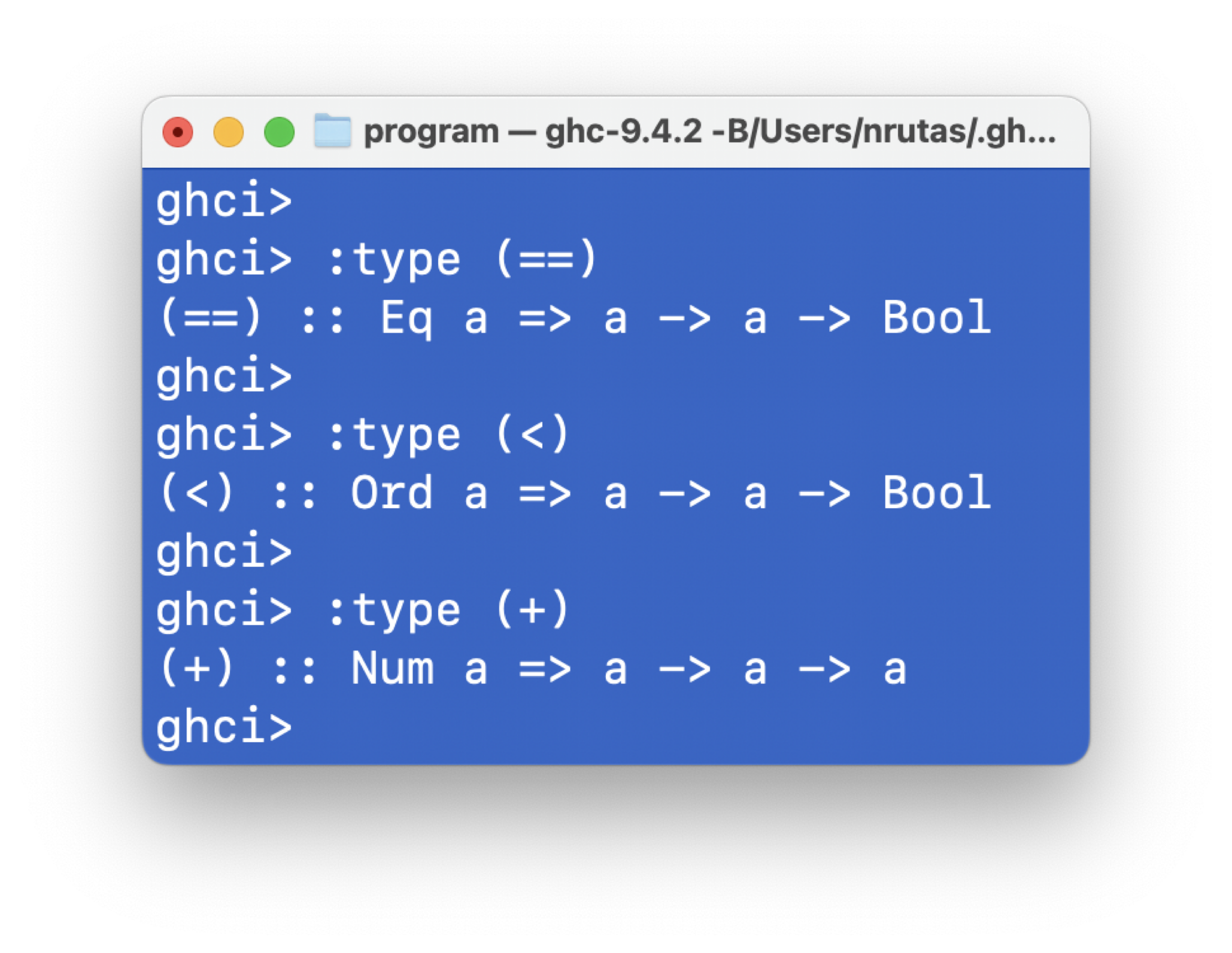
上面的截图表明:
-
相等关系运算符
==适用于所有实现了Eq的类型 -
小于关系运算符
<适用于所有实现了Ord的类型 -
加法运算符
+适用于所有实现了Num的类型
07.01 Eq
类型类 Eq 的定义如下:
class Eq a where
(==), (/=) :: a -> a -> Bool
x /= y = not (x == y)
x == y = not (x /= y)
-
对任意类型
a,-
如果:它想要成为类型类
Eq实例 -
那么:它必须要实现
==和/=这两个运算符 (两者的类型均为a -> a -> Bool)
-
-
在上面的定义中,
-
==和/=的缺省实现已经给出;但是,这是一种循环定义 -
因此,在将类型
a声明为Eq的实例时,至少要对==和/=两者之一给出定义
-
-
Prelude输出的所有基本数据类型都是Eq的实例 -
如果:一个组合类型中包含的每一个类型都是
Eq的实例,
那么:编译器可以将这个组合类型自动实现为Eq的实例。
Haskell 规范没有对实现
Eq的类型应该满足的性质给出任何规定在数学的意义上,如果类型
T实现了Eq(即,T是Eq的实例),则应满足如下性质:
自反性 (Reflexivity)
- 对于类型为
T的任何一个表达式x,满足:x == x===True对称性 (Symmetry)
- 对于类型为
T的任何两个表达式xy,满足:x == y===y == x传递性 (Transitivity)
- 对于类型为
T的任何三个表达式xyz,满足:
- 如果:
(x == y) && (y == z)===True- 那么:
x == z=== True外延性 (Extensionality)
- 对于任何函数
f :: X -> T,以及类型为X的两个表达式ab,满足:- 如果:
a == b===True- 那么:
f a == f b===TrueNegation
- 对于类型为
T的任何两个表达式xy,满足:
x /= y===not (x == y)
Eq 的最小完整实现:
(==) | (/=)
- 如果:你想将类型
T声明为Eq的一个实例,- 那么:你可以仅提供
==和/=两者之一在T上的实现
07.02 Ord
类型类 Ord 的定义依赖于另外一个类型:
data Ordering = LT | EQ | GT
-
data是 Haskell 的一个关键字 (Key Word),用于声明一个类型小和尚:
- 声明类型的关键字为什么不是
type
唐僧:
-
在 Haskell 中,关键字
type被用来声明类型的别名- “类型的别名”:就是给一个类型赋予另外一个名字
- 这样,一个类型就同时有两个名字了
- “类型的别名”:就是给一个类型赋予另外一个名字
-
我个人认为:
type的这种功能,是一个设计决策上的错误
- 声明类型的关键字为什么不是
-
这个类型定义,用 “第二章:初见函数式思维” 中的那种语言,可以表述为如下形式:
def Ordering : Type = { ctor LT : Self, ctor EQ : Self, ctor GT : Self, } -
这个类型定义,用人类语言描述,就是:
-
Ordering这个类型具有三个值LTEQGT- 类似于:
Bool这个类型具有两个值TrueFalse
- 类似于:
-
类型类 Ord 的定义如下:
class (Eq a) => Ord a where
compare :: a -> a -> Ordering
(<), (<=), (>), (>=) :: a -> a -> Bool
max, min :: a -> a -> a
compare x y = if x == y then EQ
else if x <= y then LT
else GT
x < y = case compare x y of { LT -> True; _ -> False }
x <= y = case compare x y of { GT -> False; _ -> True }
x > y = case compare x y of { GT -> True; _ -> False }
x >= y = case compare x y of { LT -> False; _ -> True }
max x y = if x <= y then y else x
min x y = if x <= y then x else y
这个定义看起来有点复杂,让我们仔细捋一捋:
class (Eq a) => Ord a where -- 这行代码含义如下:
-
声明了一个类型类
Ord -
声明了一个类型类约束
Eq a,含义如下:- 对于任何一个类型
a- 如果:
a想要成为Ord的实例 - 那么:
a必须首先成为Eq的实例
- 如果:
- 对于任何一个类型
compare :: a -> a -> Ordering
(<), (<=), (>), (>=) :: a -> a -> Bool
max, min :: a -> a -> a -- 这三行代码含义如下:
- 对于任何类型
a- 如果:
a想要成为Ord的实例, - 那么:
a就必须实现上面声明的所有 7 个函数/运算符
- 如果:
-- 其余的代码,给出了所有待实现的函数/运算符的缺省实现;不再赘述
Ord 定义了一种 全序 (Total Order) 关系,因此,满足如下性质:
-
可比性 (Comparability)
x <= y||y <= x===True
-
传递性 (Transitivity)
- 如果:
x <= y&&y <= z===True - 那么:
x <= z===True
- 如果:
-
自反性 (Reflexivity)
x <= x===True
-
反对称性 (Antisymmetry)
- 如果:
x <= y&&y <= x===True - 那么:
x == y===True
- 如果:
同时,Haskell 规范 希望:Ord 的任何实现,应保持下述性质成立:
x >= y===y <= xx < y===x <= y&&x /= yx > y===y < xx < y===compare x y == LTx > y===compare x y == GTx == y===compare x y == EQ(min x y) == (if x <= y then x else y)===True(max x y) == (if x >= y then x else y)===True
Ord的最小完整实现:compare | (<=)
- 如果:你想将类型
T声明为Ord的一个实例,- 那么:你可以仅提供
compare和<=两者之一在T上的实现
07.03 Num
类型类 Num 的定义如下:
class Num a where
(+), (-), (*) :: a -> a -> a
negate :: a -> a -- Unary negation
abs :: a -> a -- Absolute value
signum :: a -> a -- Sign of a number
fromInteger :: Integer -> a -- Conversion from an Integer
x - y = x + negate y
negate x = 0 - x
Haskell 规范没有对实现
Num的类型应该满足的性质给出任何规定在数学的意义上,如果类型
T实现了Num(即,T是Num的实例),则应满足如下性质:
+满足结合律 (Associativity)
(x + y) + z===x + (y + z)
+满足交换律 (Commutativity)
x + y===y + x
fromInteger 0是+的单位元
x + fromInteger 0===x
negate是+的逆元
x + negate x===fromInteger 0
*满足结合律
(x * y) * z===x * (y * z)
fromInteger 1是*的单位元
x * fromInteger 1===xfromInteger 1 * x===x
*对+的分配律 (Distributivity)
- a * (b + c) === (a * b) + (a * c)
- (b + c) * a === (b * a) + (c * a)
Num的最小完整实现:
(+),(*),abs,signum,fromInteger,(negate | (-))
也即:
- 前 5 个必须给出实现;
negate和(-)两者之一给出实现
本章作业
作业 01
请写出如下表达式的类型:
['a', 'b', 'c']
('a', 'b', 'c')
[(False, '0'), (True, '1')]
([False, True], ['0', '1'])
[tail, init, reverse]
- 说明:
tailinitreverse是Prelude模块输出的三个元素
作业 02
请写出如下函数的类型:
second xs = head (tail xs)
swap (x, y) = (y, x)
pair x y = (x, y)
double x = x * 2
palindrome xs = reverse xs == xs
twice f x = f (f x)
作业 03
阅读教科书,用例子 (在
ghci上运行) 展示:
Int与Integer的区别,以及
show和read的用法。
作业 04
阅读教科书和
Prelude模块文档
理解
Integral和Fractional这两个 Type Class 中定义的函数和运算符用例子 (在
ghci中运行) 展示每一个函数/运算符的用法
第 05 章:函数的定义
主要知识点:
- 利用已有函数定义新函数 / 条件表达式 / 模式匹配 / Lambda表达式 / Section
01 利用已有函数定义新函数
问题 1:判断一个整数是否是偶数
even :: Int -> Bool
even n = mod n 2 == 0
- 其中,
mod是一个已经存在的函数
问题 2:计算一个浮点数的倒数
recip :: Double -> Double
recip x = 1 / x
- 其中,
(/)是一个已经存在的函数
问题 3:将一个 list 在位置 n 分开
splitAt :: Int -> [a] -> ([a], [a])
splitAt n xs = (take n xs, drop n xs)
- 其中,
take和drop是两个已经存在的函数
02 条件表达式 (Conditional Expression)
如同大多数编程语言一样,Haskell 中也存在 条件表达式
abs :: Int -> Int
abs n = if n >= 0 then n else -n
- 函数
abs- 接收一个整数
n - 如果
n是一个非负值,则返回n;否则,返回-n
- 接收一个整数
条件表达式可以被嵌套
signum :: Int -> Int
signum n = if n < 0 then -1 else
if n == 0 then 0 else 1
- 在第一个条件表达式的
else分支中,又嵌套了一个条件表达式
在 Haskell 中,不存在 三分支或更多分支的条件表达式
- 但通过条件表达式的嵌套,可以表达出三分支/多分支的语义
在 Haskell 中,不存在 单分支条件表达式
- 在 Rust 中,在语法上确实存在单分支条件表达式,但在语义上它仍然是一个双分支表达式
03 Guarded Equation
在定义函数时,也可以通过 Guarded Equation 语法实现多分支的效果:
abs :: Int -> Int
abs n | n >= 0 = n
| otherwise = -n
-
对于函数应用
abs n,- 当条件
n >= 0成立时,abs n被定义为n - 当条件
otherwise成立时,abs n被定义为-n
- 当条件
-
otherwise是Prelude模块输出的一个元素,其定义为otherwise = true -
因此,
| otherwise = -n是一个兜底的分支
signum :: Int -> Int
signum n | n < 0 = -1
| n == 0 = 0
| otherwise = 1
- 显然,Guarded Equation 用来表达多分支结构,太方便了
04 模式匹配 (Pattern Matching)
很多函数更适合使用模式匹配进行定义:
not :: Bool -> Bool
not False = True
not True = False
-
这是模式匹配的一种极简形式,所以看起来有些无聊
即便如此,如果不使用模式匹配,你能用其他方法定义
not函数吗? -
为什么这种定义方式称为模式匹配呢?解释如下:
-
Bool是Prelude模块输出的一个类型,其定义如下:data Bool = True | False-
data是 Haskell 语言中定义类型的关键字 -
这个类型定义,用 “第二章:初见函数式思维” 中的那种语言,可以表述为如下形式:
def Bool : Type = { ctor True : Self, ctor False : Self, } -
也即,类型
Bool的值仅存在两种模式 / 构造方式 / Constructor
-
-
因此,如果在这两种模式上对
not给出了定义,自然地,就给出了not的完整定义
-
-
称上面的模式匹配是一种极简形式,原因是:
-
其中涉及的两个模式
TrueFalse没有参数- 在更一般的情况下,模式中存在参数;然后,就会很有趣
-
-
在更本质的意义上,“模式匹配” 就是 分情况讨论
利用模式匹配,定义 逻辑与 函数。三种方式:
-- 方式一
(&&) :: Bool -> Bool -> Bool
True && True = True
True && False = False
False && True = False
False && False = False
-- 方式二
(&&) :: Bool -> Bool -> Bool
True && True = True
_ && _ = False
-
下划线
_是一个通配符,可以匹配到任何值 -
上面的程序表明:模式匹配的顺序存在语义
- 即:按照定义中出现的模式匹配语句依次进行匹配
-- 方式三
(&&) :: Bool -> Bool -> Bool
True && b = b
False && _ = False
-
与前两种定义方式相比,这种方式具有更高的效率
- 原因:它完全避免了对第二个参数的评估
-
在第一个模式匹配语句中出现的
b, 称为 变量模式- 它的效果:把第二个参数绑定到局部变量
b上
- 它的效果:把第二个参数绑定到局部变量
Haskell 不支持在一个模式匹配语句中出现两个相同的变量模式。
例如,如下定义存在编译时错误:
(&&) :: Bool -> Bool -> Bool
b && b = b
_ && _ = False
-
在表面上看起来,这样的程序似乎没有问题
-
但在一般的意义上,判断两个东西是否相等,存在理论或技术上的困难性
05 序列模式 (List Pattern)
List类型的定义如下:data List a = [] | (:) a (List a)其中,出现了两个模式 / 构造方式 / Constructor:
[]:其类型为List a(:):其类型为a -> List a -> List a
Haskell 支持采用如下语法表达一个 list:
[1, 2, 3, 4, 5]这实际上是一种语法糖,去糖后,得到的表达式如下:
1 : (2 : (3 : (4 : (5 : []))))然后,Haskell 规定:运算符
:满足右结合律。因此,该表达式可进一步简化为:
1 : 2 : 3 : 4 : 5 : []删除空格后,得到更为紧凑的形式:
1:2:3:4:5:[]
定义 List 上的函数时,一种常见的模式是 x:xs。其效果是:
-
把一个 list 的第一个元素 绑定到 局部变量
x上 -
把一个 list 删除第一个元素后得到的 list 绑定到 局部变量
xs上
以下为两个示例函数:
head :: [a] -> a
head (x:_) = x
tail :: [a] -> [a]
tail (_:xs) = xs
-
只有非空 list 才能匹配到模式
x:xs上- 因此,这两个函数都是 partial function (它们在
[]上没有定义)
- 因此,这两个函数都是 partial function (它们在
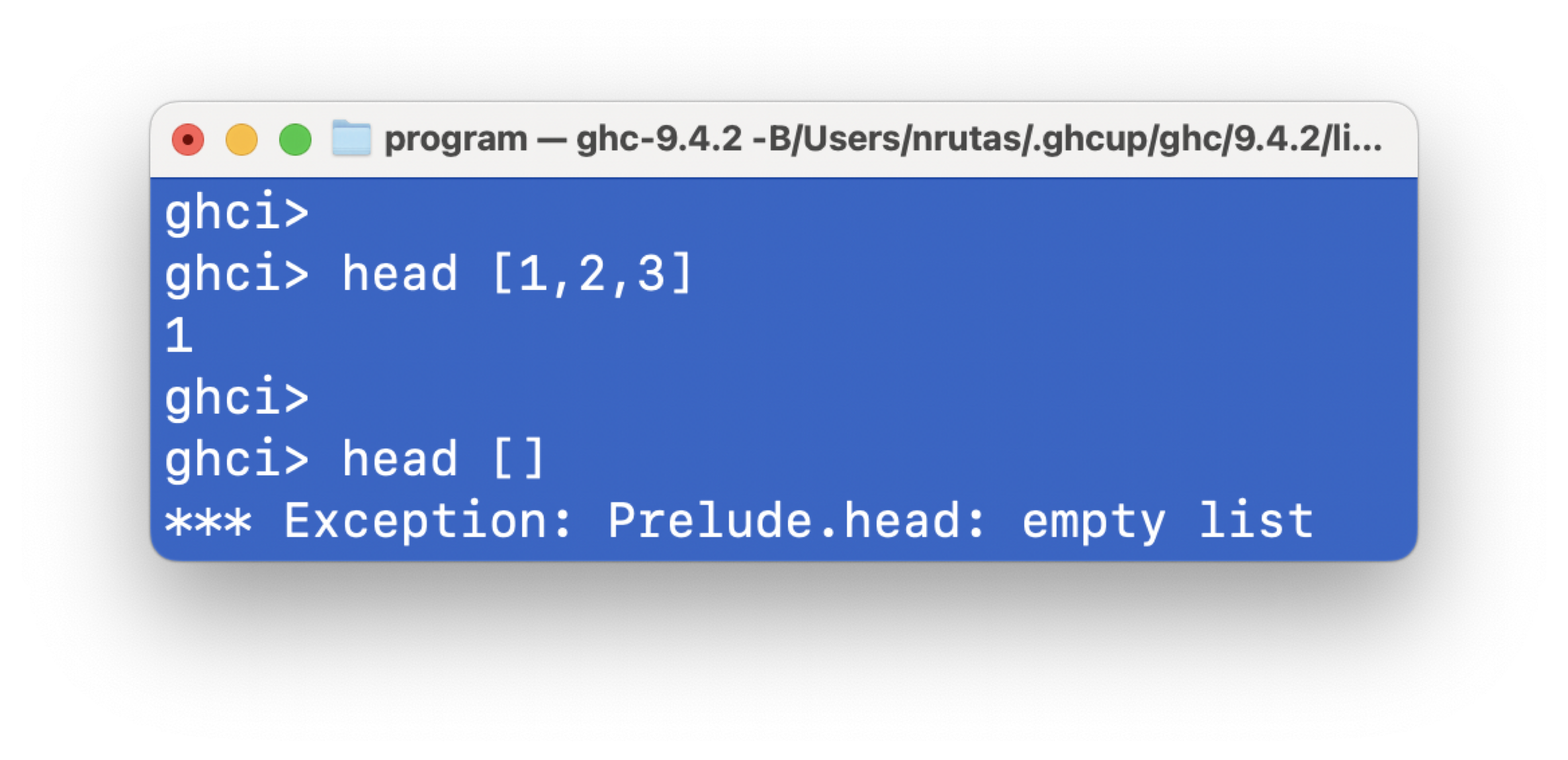
注意:以下程序会产生编译错误:
head :: [a] -> a
head x:_ = x
原因:
-
在 Haskell 中,function application (函数应用) 具有最高优先级
-
因此,
head x:_ = x会被编译器理解为(head x):_ = x
06 元组模式 (Tuple Pattern)
元组模式没有什么好说的,仅以两个示例意思一下:
-- Extract the first component of a pair.
fst :: (a, b) -> a
fst (x, _) = x
-- Extract the second component of a pair.
snd :: (a, b) -> b
snd (_, y) = y
07 λ 表达式 (Lambda Expression)
在非常肤浅的层面上,λ 表达式提供了如下能力:
- 创建匿名函数:即,创建一个没有名字的函数
例如:表达式 \x -> x + x 是一个匿名函数
- 该函数接收一个
x,返回x + x
可以把 λ 表达式中的左斜线
\理解为字母λ的 谐形字母
- 为什么要这样呢?
- 原因:键盘输入
λ不方便
λ 表达式 为柯里化函数的定义提供了更加精确的含义
-
例如:
add x y = x + y,其含义是: -
add = \x -> (\y -> x + y)
λ 表达式 可对仅使用一次的函数进行 “匿名原地构造”
odds n = map f [0..n-1]
where
f x = x * 2 + 1
-- defined in Prelude
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
-
在上面的程序中,
odds函数的定义中,出现了一个仅使用了一次的函数f -
可以使用 λ 表达式 在使用的地方对该函数进行匿名原地构造
odds n = map (\x -> x * 2 + 1) [0..n-1]
08 Operator Sections
把一个二元运算符放在一对圆括号中,就能得到该运算符对应的柯里化函数
ghci> 1 + 2
3
ghci> (+) 1 2
3
ghci> :type (+)
(+) :: Num a => a -> a -> a
甚至可以在圆括号中放置一个参数
ghci> (+ 1) 2
3
ghci> :type (+ 1)
(+ 1) :: Num a => a -> a
ghci> (1 +) 2
3
ghci> :type (1 +)
(1 +) :: Num a => a -> a
ghci> (1 -) 2
-1
ghci> :type (1 -)
(1 -) :: Num a => a -> a
但是,存在一个特殊情况
ghci> :type (- 1)
(- 1) :: Num a => a
ghci> (- 1) 2
<interactive>:5:1: error: [GHC-39999]
- 其中,
- 1被编译器理解为对1取负数
在一般意义上,对于任意二元运算符
⊕,如下三种形式称为 “section”
(⊕),(x ⊕),(⊕ y)这三种 section 的定义如下:
(⊕)===\x -> (\y -> x ⊕ y)
(x ⊕)===\y -> x ⊕ y
(⊕ y)===\x -> x ⊕ y
使用 section,可以方便地定义一些函数
-
(+ 1):后继函数 -
(1 /):倒数函数 -
(* 2):翻倍函数 -
(/ 2):减半函数
本章作业
作业 01
定义一个
safetail函数,满足如下要求:
- 该函数与
tail函数具有相同的类型- 当作用在一个非空 list 上,该函数与
tail行为相同- 当作用在一个空 list 上,该函数返回一个空 list
说明:
- 如果你愿意,可以使用函数
null :: [a] -> Bool判断 list 是否为空
作业 02
Luhn 算法被用于检查银行卡号中可能存在的简单书写错误 (例如,写错了一个数字)。
该算法的工作流程如下所述:
- 将银行卡号中的每一个数字字符视为一个独立的整数
- 从右向左,偶数位的数乘 2 (奇数位的数不变)
- 对于每一个大于 9 的数,减去 9;然后将所有的数相加
- 如果相加的结果能被 10 整除,则表示银行卡号合法;否则,非法
定义函数
luhn :: Int -> Int -> Int -> Int -> Int,对 4 位卡号的合法性进行检查。例如:ghci> luhn 1 7 8 4 Trueghci> luhn 4 7 8 3 False
第 06 章:List Comprehension
主要知识点:
- Generator / Guard / String Comprehension
01 List Comprehension
在集合论中,我们通常使用 Set Comprehension 实现 “从已有集合出发构造新的集合” 的效果:
{ x² | x ∈ { 1, 2, 3, 4, 5 } }
在 Haskell 中,一种类似的 List Comprehension 语法,可以实现 “从已有 list 出发构造新的 list” 的效果:
{ x^2 | x <- [1..5] }
上面这个表达式,从一个已有的 list [1, 2, 3, 4, 5] 出发,构造出了一个新的 list [1, 4, 9, 16, 25]。
02 Generator
在上面的示例中,x <- [1..5] 称为一个 generator。
- 因为:它能够 生成 (generate) 一些值
在一个 List Comprehension 中,可以存在多个 generators:
[ (x, y) | x <- [1, 2, 3], y <- [4, 5] ]
这个表达式构造的 list 是:
[ (1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5) ]
改变多个 generators 的顺序,会导致形成的 list 中的元素的顺序发生变化:
[ (x, y) | y <- [4, 5], x <- [1, 2, 3] ]
这个表达式构造的 list 是:
[ (1, 4), (2, 4), (3, 4), (1, 5), (2, 5), (3, 5) ]
Dependant Generator
后面的 generator 可以依赖于前面的 generator 生成的值:
[ (x, y) | x <- [1..3], y <- [x..3] ]
这个表达式构造的 list 是:
[ (1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3) ]
利用 Dependant Generator,可以给出 Prelude 模块中 concat 函数的定义:
concat :: [[a]] -> [a]
concat xss = [ x | xs <- xss, x <- xs ]
ghci> concat [ [1, 2, 3], [4, 5], [6] ]
[1,2,3,4,5,6]
03 Guard
可用使用 Guard 对 generator 生成的值进行过滤:
[ x | x <- [1..10], even x ]
这个表达式构造的 list 是:
[ 2, 4, 6, 8, 10 ]
示例: 使用 Guard,可以定义 “计算一个正整数的所有因子” 的函数:
factors :: Int -> [Int]
factors n = [ x | x <- [1..n], mod n x == 0 ]
ghci> factors 1000
[1,2,4 5,8,10,20,25,40,50,100,125,200,250,500,1000]
在此基础上,可以定义 “判断一个正整数是否是素数” 的函数:
prime :: Int -> Bool
prime n = factors n == [1,n]
ghci> prime 1
False
ghci> prime 72
False
ghci> prime 73
True
在此基础上,可以定义 “计算前 n 个素数” 的函数:
primes :: Int -> [Int]
primes n = [x | x <- [2..n], prime x]
ghci> primes 70
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67]
04 zip 函数
Prelude 模块中存在一个函数 zip,其定义如下:
zip :: [a] -> [b] -> [(a,b)]
zip [] _ = []
zip _ [] = []
zip (a:as) (b:bs) = (a,b) : zip as bs
ghci> zip ['a', 'b', 'c'] [1, 2, 3, 4]
[('a',`),('b',2),('c',3)]
你应该能够理解 zip 函数的效果:即,把两个 list 向拉链一样合并到一起
示例: 使用 zip 函数,可以定义 “计算一个 list 中所有相邻元素对” 的函数
pairs :: [a] -> [(a,a)]
pairs xs = zip xs (tail xs)
ghci> pairs [1..10]
[(1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,8),(8,9),(9,10)]
示例: 使用 zip 函数,可以定义 “判断一个 list 是否处于有序 (从小到大) 状态” 的函数
sorted :: Ord a => [a] -> Bool
sorted xs = and [ x <= y | (x, y) <- pairs xs ]
ghci> sorted [1..10]
True
ghci> sorted [1,3,2,4]
False
示例: 使用 zip 函数,可以定义 “计算一个值在一个 list 中所有出现的位置” 的函数
positions :: Eq a => a -> [a] -> [Int]
positions x xs = [ i | (x',i) <- zip xs [0..], x == x' ]
05 String Comprehension
在 Haskell 中,一个 字符串字面量 (String Literal) 是一个由一对双引号包围的字符序列。
"abcd" :: String
其中,类型 String 是类型 [Char] 的别名。因此,上述声明等价于:
['a', 'b', 'c', 'd'] :: [Char]
因为 String 是一种特殊的 List 类型,所以任何定义在 List 类型上的多态函数也适用于 String 类型。
ghci> length "abcde"
5
ghci> take 3 "abcde"
"abc"
ghci> zip "abcd" [1, 2, 3, 4]
[('a',1),('b',2),('c',3),('d',4)]
类似地,List Comprehension 也可用于定义作用在 String 上的函数。例如,下面给出了 “计算字符在字符串中出现次数” 的函数定义:
count :: Char -> String -> Int
count x xs = length [ x' | x' <- xs, x == x' ]
ghci> count 'g' "googlegod"
3
06 问题示例:凯撒加密
为了对字符串文本进行加密,凯撒发明了如下的加密方式:
-
把一个英文字母替换为它在字母表中后面的第 3 个字母
-
如果到达了字母表的末尾 (即:字母
z),则回转到第一个字母a- 也即,字母
z的后继字母是a
- 也即,字母
下面,我们按照这种方式,分别定义 加密 和 解密 两个函数。
ghci> :type encode
encode :: Int -> String -> String
ghci> encode 3 "haskell is fun"
"kdvnhoo lv ixq"
ghci> encode (-3) "kdvnhoo lv ixq"
"haskell is fun"
ghci> :type crack
crack :: String -> String
ghci> crack "kdvnhoo lv ixq"
"haskell is fun"
加密 / encode
import Data.Char(ord, chr, isLower)
-- ord :: Char -> Int // 将字符转换为编码值
-- chr :: Int -> Char // 将编码值转换为字符
-- isLower :: Char -> Bool // 判断字符是否为小写字母
encode :: Int -> String -> String
encode n xs = [ shift n x | x <- xs ]
shift :: Int -> Char -> Char
shift n c | isLower c = int2let $ mod (let2int c + n) 26
| otherwise = c
let2int :: Char -> Int
let2int c = ord c - ord 'a'
int2let :: Int -> Char
int2let n = chr $ ord 'a' + n
解密 / crack
对凯撒加密后的字符串进行解密的关键:
- 在英文语料中,不同字母出现的频率是不同的
下面定义 table 依次记录了 26 个英文字母的出现百分比:
table :: [Float]
table = [ 8.1, 1.5, 2.8, 4.2, 12.7, 2.2, 2.0, 6.1, 7.0,
0.2, 0.8, 4.0, 2.4, 6.7, 7.5, 1.9, 0.1, 6.0,
6.3, 9.0, 2.8, 1.0, 2.4, 0.2, 2.0, 0.1 ]
chi-square statistic:一种对一组 期望频率 (expected frequencies) 和 一组 观察频率 (observed frequencies) 进行比较的标准方法。
假设存在两个长度为 n 的频率序列: 1.期望频率序列 es;2.观察频率序列 os。则两者的 chi-square statistic 定义如下:
\[ \sum_{i=0}^{n - 1} \frac{(os[i] - es[i])^2}{es[i]}\]
#![allow(unused)] fn main() { import Data.Char(ord, chr, isLower) crack :: String -> String crack xs = encode (- factor) xs where factor = position (minimum chitab) chitab -- minimum: a function exported by Prelude -- 计算每种加密偏移量下的chisqr chitab = [ chisqr (rotate n table') table | n <- [0..25] ] -- 计算密文中字母的出现频率 table' = freqs xs table :: [Float] table = [ 8.1, 1.5, 2.8, 4.2, 12.7, 2.2, 2.0, 6.1, 7.0, 0.2, 0.8, 4.0, 2.4, 6.7, 7.5, 1.9, 0.1, 6.0, 6.3, 9.0, 2.8, 1.0, 2.4, 0.2, 2.0, 0.1 ] position :: Eq a => a -> [a] -> Int rotate :: Int -> [a] -> [a] freqs :: String -> [Float] chisqr :: [Float] -> [Float] -> Float }
本章作业
作业 01
请给出凯撒解密函数的完整定义:即,把上述定义中缺失的函数补充完整
说明:
仅考虑 “明文中仅包含小写字母和空格” 的情况
自行学习如何使用 Prelude 中的如下函数实现从整数类型到浮点数类型的转换
fromIntegral :: (Integral a, Num b) => a -> b
作业 02
称一个三元组
(x, y, z)为 毕达哥拉斯 (Pythagorean) 三元组,如果其满足如下条件:
x² + y² === z²使用 List Comprehension,定义一个函数:
pyths :: Int -> [(Int, Int, Int)]该函数接收一个正整数
n,返回区间[1..n]中所有的毕达哥拉斯三元组 (返回的三元组序列按照从小到大的顺序排列)例如:
ghci> pyths 5 [(3,4,5),(4,3,5)]
作业 03
称一个正整数为完美 (perfect) 数,如果它等于自身所有因子 (不含自身) 的和
使用 List Comprehension,定义一个函数:
perfects :: Int -> [Int]该函数接收一个正整数
n,返回区间[1..n]中的所有完美数 (返回的序列按照从小到大的顺序排列)例如:
ghci> perfects 500 [6, 28, 496]
作业 04
对于两个长度为
n的整数序列xsys,两者的的点积 (Scalar Product) 定义如下:\[ \sum_{i=0}^{n-1} (xs[i] * ys[i])\]
使用 List Comprehension,定义一个 “计算两个整数序列的点积” 的函数:
第 07 章:递归函数
01 递归函数
在前文中已经看到,可以基于已有的函数定义新的函数:
fac :: Int -> Int
fac n = product [1..n]
在很多情况下,一个函数可以通过自身对自身进行定义:
fac :: Int -> Int
fac 0 = 1
fac n = n * fac (n-1)
这类函数称为 递归函数 (Recursive Function)。
02 为什么需要递归函数?
-
一些函数,其递归定义方式更为简洁
-
一些函数,其定义本身就天然存在递归
-
在一些情况下,递归定义的函数,其数学性质更易于证明
03 List 上的递归函数
递归不仅适用于整数类型,也适用于 List 以及其他类型。
示例:List 中元素的乘积
product :: Num a => [a] -> a
product [] = 1
product (n:ns) = n * product ns
示例:List 的长度
length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs
示例:List 逆序
reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
示例:插入排序
isort :: Ord a => [a] -> [a]
isort [] = []
isort (x:xs) = insert x (isort xs)
insert :: Ord a => a -> [a] -> [a]
insert x [] = [x]
insert x (y:ys) | x <= y = x:y:ys
| otherwise = y:(insert x ys)
04 多参数递归
具有多个参数的函数,也可以进行递归定义。
示例:zip 函数
zip :: [a] -> [b] -> [(a,b)]
zip [] _ = []
zip _ [] = []
zip (x:xs) (y:ys) = (x, y) : zip xs ys
示例:drop 函数
drop :: Int -> [a] -> [a]
drop 0 xs = xs
drop _ [] = []
drop n (_:xs) = drop (n-1) xs
示例:序列拼接函数
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)
05 多重递归 (Multiple Recursion)
所谓 多重递归,指的是:在定义一个函数时,对函数自身进行了多次递归调用。
fib :: Int -> Int
fib 0 = 0
fib 1 = 1
fib n = fib (n - 2) + fib (n - 1)
qsort :: Ord a => [a] -> [a]
qsort [] = []
qsort (x:xs) = qsort smaller ++ [x] ++ qsort larger
where
smaller = [a | a <- xs, a <= x]
larger = [b | b <- xs, b > x]
qsort [3, 2, 4, 1, 5]
=== qsort [2,1] ++ [3] ++ qsort [4,5]
=== qsort [1] ++ [2] ++ qsort [] ++ [3] ++ qsort [] ++ [4] ++ qsort [5]
=== [1] ++ [2] ++ [] ++ [3] ++ [] ++ [4] ++ [5]
06 互递归 (Mutual Recursion)
所谓 互递归,指的是:在定义两或多个函数时,这些函数通过相互调用对方进行定义。
even :: Int -> Bool
even 0 = True
even n = odd (n-1)
odd :: Int -> Bool
odd 0 = False
odd n = even (n-1)
本章作业
作业 01
在不查看 Prelude 源码的情况下,使用递归定义如下函数:
- 判断
[Bool]类型的一个值中的所有元素是否都为Trueand :: [Bool] -> Bool- 将类型
[[a]]的一个值中包含的所有 list 拼接为一个 listconcat :: [[a]] -> [a]- 获得一个 list 中编号为
n的元素 (从0开始编号)(!!) :: [a] -> Int -> a- 生成一个包含
n个重复元素的 listreplicate :: Int -> a -> [a]- 判断一个元素是否包含在一个 list 中
elem :: Eq a => a -> [a] -> Bool
作业 02
采用递归的方式定义如下函数:
merge :: Ord a => [a] -> [a] -> [a]该函数接收两个已经处于从小到大排序状态的 list,然后把其中包含的所有元素归并成一个保持排序状态的 list。
例如:
ghci> merge [2,5,6] [1,3,4] [1,2,3,4,5,6]
作业 03
采用递归的方式定义归并排序函数:
msort :: Ord a => [a] -> [a]它的递归定义包含两条规则:
- 长度小于 2 的 list 已经处于排序状态
- 对于长度大于 1 的 list,将其从中间断开,形成两个更短的 list,然后:
- 对这两个更短的 list 分别进行归并排序
- 将排序后形成的两个 list 进行归并
第 08 章:高阶函数
“高阶函数” 的英文为: Higher-order Function
01 高阶函数
所谓 “高阶函数”,指的是:这个函数的某个参数或返回值是一个函数。
twice :: (a -> a) -> a -> a
twice f x = f (f x)
上面这个 twice 是一个高阶函数,原因如下:
-
这个函数接收的第一个参数是一个函数 (类型为
a -> a);或者 -
这个函数接收第一个参数后返回一个函数 (类型为
a -> a)
02 为什么需要高阶函数
-
一些常用的程序设计模式 (Common Programming Idiom) 可以表示为高阶函数
-
领域特定语言 (Domain Specific Language) 的很多成分,也可以表示为高阶函数
-
高阶函数具有的代数性质,可用于程序性质证明
03 map 函数
Prelude 模块中的 map 是一个经典的高阶函数,其功能是把一个函数作用到一个 list 中的每个元素上。
map :: (a -> b) -> [a] -> [b]
ghci> map (+1) [1, 2, 3, 4, 5]
[2, 3, 4, 5, 6]
map 函数可以使用 List Comprehension 进行简洁的定义:
map :: (a -> b) -> [a] -> [b]
map f xs = [f x | x <- xs]
map 函数也可以使用递归方式进行定义:
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
04 filter 函数
Prelude 模块中的 filter 是一个经典的高阶函数,其功能是把 list 中不满足指定条件的元素删除。
filter :: (a -> Bool) -> [a] -> [a]
ghci> filter even [1..10]
[2,4,6,8,10]
filter 函数可以使用 List Comprehension 进行定义:
filter :: (a -> Bool) -> [a] -> [a]
filter pred xs = [x | x <- xs, pred x]
filter 函数也可以使用递归方式进行定义:
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter pred (x:xs)
| pred x = x : filter pred xs
| otherwise = filter pred xs
05 List 上的 foldr 函数
一些定义在 list 上的函数,可以使用如下的递归模式进行定义:
f [] = v
f (x:xs) = x ⊕ f xs
其含义是:
-
函数
f将一个空 list[]映射到值v -
函数
f将一个非空 list(x:xs)映射为一个函数(⊕)作用到x和f xs上
请看下面的三个示例:
sum [] = 0
sum (x:xs) = x + sum xs
sum = foldr (+) 0
product [] = 1
product (x:xs) = x * product xs
product = foldr (*) 1
and [] = True
and (x:xs) = x && and xs
and = foldr (&&) True
在 Haskell 中,foldr 是 type class Foldable 中的一个函数:
class Foldable t where
foldr :: (a -> b -> b) -> b -> t a -> b
...
-
在一般意义上,
foldr是定义在一种结构 (structure) 上的满足右结合律的折叠 (fold) 操作,且具有惰性求值的特点- “结构”:理解为为 “类型” 即可;每一种类型都可以视为一种结构
- “惰性求值”:大致可以理解为,当前用不到的计算结果,绝对不会去计算
-
在 List 这种结构上的
foldr,具有如下行为:foldr f z [x1, x2, ..., xn] === x1 `f` (x2 `f` ... (xn `f` z) ...) -- 因为 `f` 满足右结合律,所以 === x1 `f` x2 `f` ... xn `f` z === f x1 (f x2 (... (f xn z) ...)) -
在对上面
===右侧的表达式进行求值时,按照惰性求值的策略,首先对最外层函数应用进行求值- 因此,如果函数
f对其第二个参数也具有惰性求值的行为,那么,即使foldr的三个参数是一个 infinite list,foldr函数也有可能终止
- 因此,如果函数
List 上的 foldr 可以采用递归方式进行定义:
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f v [] = v
foldr f v (x:xs) = f x (foldr f v xs)
在宏观上,可以将 List 上的 foldr 理解为:将一个 list 中的 [] 替换为一个指定的值;同时,将所有的 (:) 替换为一个指定的函数
若干示例:
sum = foldr (+) 0
sum [1, 2, 3]
=== foldr (+) 0 [1, 2, 3]
=== foldr (+) 0 (1 : (2 : (3 : [])))
=== 1 + (2 + (3 + 0 ))
=== 6
product = foldr (*) 1
product [1, 2, 3]
=== foldr (*) 1 [1, 2, 3]
=== foldr (*) 1 (1 : (2 : (3 : [])))
=== 1 * (2 * (3 * 1 ))
=== 6
length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs
length [1, 2, 3]
=== length (1 : (2 : (3 : [])))
=== 1 + (1 + (1 + 0 ))
=== 3
length :: [a] -> Int
length = foldr (⊕) 0 where
_ ⊕ n = 1 + n
length [1, 2, 3]
=== foldr (⊕) 0 (1 : (2 : (3 : [])))
=== 1 ⊕ (2 ⊕ (3 ⊕ 0 ))
=== 1 + (1 + (1 + 0 ))
=== 3
reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
reverse [1, 2, 3]
=== reverse (1 : (2 : (3 : [])))
=== (([] ++ [3]) ++ [2]) ++ [1]
=== [3, 2, 1]
reverse :: [a] -> [a]
reverse = foldr (⊕) [] where
x ⊕ xs = xs ++ [x]
reverse [1, 2, 3]
=== foldr (⊕) [] (1 : (2 : (3 : [])))
=== 1 ⊕ (2 ⊕ (3 ⊕ []))
=== (([] ++ [3]) ++ [2]) ++ [1]
=== [3, 2, 1]
最后,可以看到,函数 (++) 采用 foldr 进行定义非常简洁:
(++) :: [a] -> [a] -> [a]
(++ ys) = foldr (:) ys
遗憾的是,Haskell 目前并不支持这种定义方式。
以下是两种可以通过编译的定义方式:
(++) :: [a] -> [a] -> [a]
(++) xs ys = foldr (:) ys xs
(++) :: [a] -> [a] -> [a]
(++) = flip $ foldr (:)
-- flip 是 Prelude 中的一个函数,其定义如下:
flip :: (a -> b -> c) -> b -> a -> c
flip f x y = f y x
(++) xs ys
=== (flip $ foldr (:) ) xs ys
=== (flip (foldr (:))) xs ys
=== flip (foldr (:)) xs ys
=== (foldr (:)) ys xs
=== foldr (:) ys xs
为什么需要 foldr
-
一些函数,使用
foldr定义,非常简洁 -
foldr具有的代数性质,可以用于程序性质证明 -
使用
foldr定义的函数便于进行性能优化
06 List 上的 foldl 函数
在 List 上的一些函数,也可以采用左结合的方式进行递归定义。共性模式如下:
f v [] = v
f v (x:xs) = f (v ⊕ x) xs
List 上的 foldl 函数可以采用递归方式定义:
foldl :: (b -> a -> b) -> b -> [a] -> b
foldl f v [] = v
foldl f v (x:xs) = foldl f (f v x) xs
与 foldl 类似,在 Haskell 中,foldr 是 type class Foldable 中的一个函数:
class Foldable t where
foldr :: (a -> b -> b) -> b -> t a -> b
foldl :: (b -> a -> b) -> b -> t a -> b
...
-
在一般意义上,
foldl是定义在一种结构 (structure) 上的满足左结合律的折叠 (fold) 操作,且具有惰性求值的特点 -
在 List 这种结构上的
foldl,具有如下行为:foldl f z [x1, x2, ..., xn] === (((z `f` x1) `f` x2)...) `f` xn -- 因为 `f` 满足左结合律,所以 === z `f` x1 `f` x2 ... `f` xn === f (... (f (f z x1) x2) ...) xn -
在对上面 === 右侧的表达式进行求值时,按照惰性求值的策略,首先对最外层函数应用进行求值
- 因此,如果
foldl的三个参数是一个 infinite list,则foldl函数 不会终止
- 因此,如果
-
如果想要一个传统高效的
foldl,可以使用foldl'函数
07 Prelude 中的若干高阶函数
函数组合
(.) :: (b -> c) -> (a -> b) -> a -> c
(.) f g = \x -> f $ g x
-
其中,
\x -> f $ g x是 Haskell 中声明匿名函数的语法 -
使用示例:
odd :: Int -> Bool odd = not . even
all 函数
all 函数计算一个结构中的所有元素是否都满足一个指定的条件 (谓词)
all :: Foldable t => (a -> Bool) -> t a -> Bool
在 List 上,all 函数的定义如下:
all :: (a -> Bool) -> [a] -> Bool
all p xs = and [p x | x <- xs]
any 函数
any 函数计算一个结构中的所有元素中是否存在至少一个满足指定条件的元素
any :: Foldable t => (a -> Bool) -> t a -> Bool
在 List 上,any 函数的定义如下:
any :: (a -> Bool) -> [a] -> Bool
any p xs = or [p x | x <- xs]
takeWhile 函数
takeWhile 函数持续取出一个 list 中的元素,直到遇到第一个不满足指定条件的元素
takeWhile :: (a -> Bool) -> [a] -> [a]
takeWhile _ [] = []
takeWhile p (x:xs)
| p x = x : takeWhile p xs
| otherwise = []
ghci> takeWhile (/= ' ') "abc def"
"abc"
dropWhile 函数
与 takeWhile 相反,dropWhile 函数持续地忽略一个 list 中的元素,直到遇到第一个不满足指定条件的元素
dropWhile :: (a -> Bool) -> [a] -> [a]
dropWhile _ [] = []
dropWhile p xs@(x:xs')
| p x = dropWhile p xs'
| otherwise = xs
其中出现了一种新的语法
xs@(x:xs')。你猜猜这种语法的效果是什么?
08 应用 01:Binary String Transmitter
2 进制数 转换到 10 进制数
效果:
ghci> bin2int [1, 0, 1, 1]
13
- 待转换的二进制数放置在 list 中,且:低位在左,高位在右
定义方式一:
type Bit = Int
-- 将 Bit 作为类型 Int 的别名
bin2int :: [Bit] -> Int
bin2int bits = sum [ w * b | (w, b) <- zip weights bits ]
where weights = iterate (* 2) 1
-- iterate is defined in Prelude
iterate :: (a -> a) -> a -> [a]
iterate f x = x : iterate f (f x)
定义方式二:
type Bit = Int
bin2int :: [Bit] -> Int
bin2int = foldr (\x y -> x + 2 * y) 0
10 进制数 转换到 8 位 2 进制数
效果:
ghci> int2bin8 13
[1, 0, 1, 1, 0, 0, 0, 0]
定义:
int2bin :: Int -> [Bit]
int2bin 0 = []
int2bin n = mod n 2 : int2bin (div n 2)
make8 :: [Bit] -> [Bit]
make8 bits = take 8 $ bits ++ repeat 0
-- repeat is defined in Prelude
repeat :: a -> [a]
repeat x = xs where xs = x : xs
int2bin8 :: Int -> [Bit]
int2bin8 = make8 . int2bin
文字序列编码
效果:
ghci> encode "abc"
[1,0,0,0,0,1,1,0,0,1,0,0,0,1,1,0,1,1,0,0,0,1,1,0]
定义:
encode :: String -> [Bit]
encode = concat . map (make8 . int2bin . ord)
2 进制序列解码
效果:
ghci> decode [1,0,0,0,0,1,1,0,0,1,0,0,0,1,1,0,1,1,0,0,0,1,1,0]
"abc"
定义:
decode :: [Bit] -> String
decode = map (chr . bin2int) . chop8
chop8 :: [Bit] -> [[Bit]]
chop8 [] = []
chop8 bits = take 8 bits : chop8 (drop 8 bits)
09 应用 02.01:投票算法 之 First Past the Post
在这种投票系统中,每一个投票者仅可以投一个候选项。获得票数最多的候选项,成为获胜者。
以下给出投票结果的一个示例:
votes :: [String]
votes = ["Red", "Blue", "Green", "Blue", "Blue", "Red"]
编写两个函数 result 和 winner,实现如下效果:
ghci> result votes
[(1,”Green"),(2,"Red"),(3,"Blue")]
ghci> :type result
result :: Ord a => [a] -> [(Int, a)]
ghci> winner votes
"Blue"
ghci> :type winner
winner :: Ord a => [a] -> a
定义:
result :: Ord a => [a] -> [(Int, a)]
result vs = sort [ (count v vs, v) | v <- rmdups vs ]
-- The sort function is defined in Data.List
rmdups :: Eq a => [a] -> [a]
rmdups [] = []
rmdups (x:xs) = x : filter (/= x) (rmdups xs)
count :: Eq a => a -> [a] -> Int
count x = length . filter (== x)
winner :: Ord a => [a] -> a
winner = snd . last . result
09 应用 02.02:投票算法 之 Alternative Vote
在这种投票系统中,每一个投票者:
-
可以给任意多个候选项进行投票
-
但是需要给所投的候选项排序,从而表明自己对所投候选项的偏好
- 排序在第 1 位的候选项,为第 1 选择;排序在第 2 位的候选项,为第 2 选择;以此类推
下面给出了记录所有投票者投票结果的示例 (包含 5 个投票者的投票结果):
ballots :: [[String]]
ballots = [["Red", "Green"],
["Blue"],
["Green", "Red", "Blue"],
["Blue", "Green", "Red"],
["Green"]]
编写一个 winner 函数,实现如下效果:
ghci> winner ballots
"Green"
ghci> :type winner
winner :: Ord a => [[a]] -> a
获胜者的确定规则:
-
如果某个投票者的投票结果为空,则将其从全部投票结果中删除
-
在所有投票者的第一选择中,确定得票数最少的候选项,然后将该候选项从全部投票结果中删除
-
重复执行上述步骤 1 和 2,直到仅存在一个候选项;该候选项即为最终获胜者
下面,我们以 ballots 为例,展示整个计算过程:
ballots :: [[String]]
ballots = [["Red", "Green"],
["Blue"],
["Green", "Red", "Blue"],
["Blue", "Green", "Red"],
["Green"]]
-
执行步骤 1:
- 因为不存在为空的投票结果,所以
ballots没有发生变化
- 因为不存在为空的投票结果,所以
-
执行步骤 2:
- 在所有第 1 选择中,得票最少的是
"Red";所以,将所有"Red"从ballots中删除
ballots :: [[String]] ballots = [["Green"], ["Blue"], ["Green", "Blue"], ["Blue", "Green"], ["Green"]] - 在所有第 1 选择中,得票最少的是
-
执行步骤 1:
- 因为不存在为空的投票结果,所以
ballots没有发生变化
- 因为不存在为空的投票结果,所以
-
执行步骤 2:
- 在所有第 1 选择中,得票最少的是
"Blue";所以,将所有"Blue"从ballots中删除
ballots :: [[String]] ballots = [["Green"], [], ["Green"], ["Green"], ["Green"]] - 在所有第 1 选择中,得票最少的是
-
执行步骤 1:
- 删除所有为空的投票
ballots :: [[String]] ballots = [["Green"], ["Green"], ["Green"], ["Green"]] -
只剩下一个候选项
"Green";产生获胜者
定义:
winner :: Ord a => [[a]] -> a
winner bs = case rank $ filter (/= []) bs of
[c] -> c
(c:cs) -> winner $ map (filter (/= c)) bs
rank :: Ord a => [[a]] -> [a]
rank = map snd . result . map head
本章作业
作业 01
对
[f x | x <- xs, p x]使用函数map和filter进行表达
作业 02
使用
foldr对map f和filter p进行定义
作业 03
对 binary string transmitter 示例进行改写,实现 “检测传输错误” 的功能。
具体而言,采用 “奇偶校验位” 对传输错误进行检测:
- 在编码时,每 8 个二进制位添加 1 个奇偶校验位
- 当这 8 个二进制位 包含奇数个
1时,将校验位设为1;否则,设置为0- 在解码时,对每 9 个二进制位进行校验
- 若奇偶校验位正确,则将校验位抛弃;否则,输出错误,并终止程序
提示:
- 库函数
error :: String -> a具有 “输出错误信息并终止程序” 的效果- 该函数的返回值类型是一个类型参数,所以它可以在任何函数中使用,而不会产生类型错误
第 09 章:声明类型和类簇
01 类型别名的声明
在 Haskell 中,可以通过 type 关键字为一个已经存在的类型声明一个 别名。
type String = [Char]
其中:
-
[Char]是一个已经存在的类型,而String仅仅是它的一个别名 -
所谓 “别名”,就是另一个名称,或者称为 同义词
引入别名的主要目的:为一个已经存在的类型赋予更明确的含义:
type Position = (Int, Int)
-
原本的类型
(Int, Int)本身并没有 “位置” 这种专有含义 -
通过将其命名为
Position,可以更直接地明确 “用二元组表示二维位置” 的含义origin :: Position origin = (0, 0) left :: Position -> Position left (x, y) = (x - 1, y)
别名声明,也可以具有参数。
type Pair a = (a, a) mult :: Pair Int -> Int mult (m, n) = m * n copy :: a -> Pair a copy x = (x, x)
在声明一个别名时,在等号
=的右侧可以出现已经定义的其他别名type Position = (Int, Int) type Trans = Position -> Position
但是,别名不支持递归定义。因此,下述定义会产生编译错误:
type Tree = (Int, [Tree])- 即便这种定义成立,类型为
Tree的元素似乎也有些无聊
- 即便这种定义成立,类型为
02 类型的声明
在 Haskell 中,可以通过 data 关键字声明新的类型。
data Bool = False | True
-
Bool一个新定义的类型,它具有两个值:FalseTrue-
Bool是一个平凡 (trivial) 的 Type Constructor -
False和True是两个平凡 (trivial) 的 Data Constructor -
这里的 平凡 (trivial),指的是没有参数
- 马上就会看到带有参数的 Type/Data Constructor
-
-
在 Haskell 中,Type/Data Constructor 的标识符的首字符必须是大写字母
使用 “初见函数式思维” 一章中引入的那种语言,上述
Bool类型定义为def Bool : Type = { ctor False : Self ctor True : Self }注意:
- 关键字
ctor是英文单词 constructor 的缩写
自定义的类型和值,其使用方式与标准库中定义的类型和值 完全相同
data Answer = Yes | No | Unknown
answers :: [Answer]
answers = [Yes, No, Unknown]
flip :: Answer -> Answer
flip Yes = No
flip No = Yes
flip Unknown = Unknown
Data Constructor 可以具有参数。
data Shape = Circle Float | Rect Float Float
square :: Float -> Shape
square n = Rect n n
area :: Shape -> Float
area (Circle r) = pi * r * r
area (Rect x y) = x * y
使用 “初见函数式思维” 一章中引入的那种语言,上述
Shape类型定义为def Shape : Type = { ctor Circle : Float -> Self ctor Rect : Float -> Float -> Self }更为神奇的是,在 Haskell 中:
你确实可以把
Circle视为一个类型为Float -> Shape的函数你确实可以把
Rect视为一个类型为Float -> Float -> Shape的函数如果你不相信,可以写程序测试一下。
有参数的 Data Constructor 才是一种 非平凡 (non-trivial) 的 Data Constructor。
Type Constructor 也可以具有参数。
data Maybe a = Nothing | Just a
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv m n = Just $ div m n
safehead :: [a] -> Maybe a
safehead [] = Nothing
safehead xs = Just $ head xs
使用 “初见函数式思维” 一章中引入的那种语言,上述
Maybe定义为def Maybe : Type -> Type = [T] { ctor Nothing : Self ctor Just : T -> Self }
有参数的 Type Constructor 才是一种 非平凡 (non-trivial) 的 Type Constructor。
03 递归类型
在 Haskell 中,新的类型可以通过自身进行递归定义。例如:
data Nat = Zero | Succ Nat
-
Nat是一个新的类型,它具有两个 Data Constructor:Zero :: NatSucc :: Nat -> Nat -
也即,类型
Nat的值,或者是Zero,或者具有形式Succ n(其中,n :: Nat) -
也即,
Nat具有如下无穷多个值Zero,Succ Zero,Succ (Succ Zero),Succ (Succ (Succ Zero)), ...
-
我们可以将
Nat视为 自然数;其中-
Zero表示0 -
Succ表示函数(1 + )
-
-
例如:
Succ $ Succ $ Succ Zero表示自然数(1+) $ (1+) $ (1+) Zero === 3
小和尚:
- 这不就是 “结绳计数” 吗?
唐僧:
-
确实如此
-
不过,我们研究的是自然数的本质,而不是自然数的表现形式
-
我们熟悉的自然数,其实是自然数的一种表现形式:即,十进制表现形式
-
这种表现形式 (十进制) 过于复杂:与本质相比,有点喧宾夺主的感觉
-
data Nat = Zero | Succ Nat
-
使用递归,可以方便地实现
Nat与Int两者之间的相互转换nat2int :: Nat -> Int nat2int Zero = 0 nat2int (Succ n) = 1 + nat2int n int2nat :: Int -> Nat int2nat 0 = Zero int2nat n = Succ $ int2nat $ n - 1 -- 注意:当把 int2nat 做用到一个负数上,就出大问题了 -
自然数的加法:定义一 (以
Int为媒介)add :: Nat -> Nat -> Nat add m n = int2nat $ nat2int m + nat2int n -
自然数的加法:定义一 (直接定义)
add :: Nat -> Nat -> Nat add Zero n = n add (Succ m) n = Succ $ add m n或者
add :: Nat -> Nat -> Nat add m Zero = m add m (Succ n) = Succ $ add m n
04 示例:用于表示算术运算表达式的类型
考虑一种简单的算术运算表达式:由整数、加法、乘法形成的算术表达式。
我们可以定义一种类型,用于表示这种算法运算表达式;也即:
-
这种类型的一个值,一定表示了一个算术运算表达式
-
这样的一个表达式,可以表示为这种类型的一个值
data Expr = Val Int | Add Expr Expr | Mul Expr Expr
-
注意:这个类型具有三个 Data Constructor
-
Val :: Int -> Expr -
Add :: Expr -> Expr -> Expr -
Mul :: Expr -> Expr -> Expr
-
-
例如:
1 + (2 * 3)被表示为Add (Val 1) (Mul (Val 2) (Val 3))如果你再给出如下定义:
(⊕) :: Expr -> Expr -> Expr (⊕) = Add (⊗) :: Expr -> Expr -> Expr (⊗) = Mul那么:
1 + (2 * 3)可以表示为Val 1 ⊕ (Val 2 ⊗ Val 3)如前所述:
Add和Mul这两个 Data Constructor 确实是函数
利用递归,我们可以定义作用在 Expr 上的各种函数:
data Expr = Val Int | Add Expr Expr | Mul Expr Expr
size :: Expr -> Int
size (Val n) = 1
size (Add x y) = size x + size y
size (Mul x y) = size x + size y
eval :: Expr -> Int
eval (Val n) = n
eval (Add x y) = eval x + eval y
eval (Mul x y) = eval x * eval y
对于类型 Expr,是否存在一个相应的 fold 函数呢?
-
如果你对
Natural和List上的fold函数有深刻理解,那么,这是一件相对简单的事情- 即,把这三个 Data Constructor 替换为恰当的函数
不妨将 Expr 上的 fold 函数命名为 folde。可知,其类型如下:
folde :: (Int -> a) -> (a -> a -> a) -> (a -> a -> a) -> Expr -> a
如何定义该函数,是本章的一个作业题
基于 folde,可以对刚才定义的两个函数 size 和 eval 进行重新定义:
|
|
|
|
05 newtype 声明
如果:一个类型仅具有一个 Data Constructor,且 这个 Data Constructor 仅具有一个参数,
那么:可以使用 newtype 对这种类型进行声明。
例如:
newtype Nat = N Int
相比较另外两种定义方式,上述定义既具有更高的运行效率,还具有更好的类型安全性:
-
data Nat = N Int:运行效率低-
Int 值总是被包裹在
N这样一个盒子里;每次想要获得 Int 值,必须首先打开盒子 -
反之,
newtype Nat = N Int中的N会被编译器优化掉,因此不存在运行时成本
-
-
type Nat = Int:类型安全性差-
可能会把一个负数误用为自然数
-
反之,
N Int这种语法,强制要求程序员写出N,从而提醒他/她后面千万不能放负数
-
这是一种实现上的细节。你需要在理解了 Haskell 的类型在内存中的 Representation 和 Layout 后,可能才会明白
newtype的效果。
06 类簇及其实例的声明
声明一个类簇:
class Eq a where
(==), (/=) :: a -> a -> Bool
x /= y = not (x == y)
x == y = not (x /= y)
{-# MINIMAL (==) | (/=) #-}
-- 请自己课后确认一下:上面这一行代码,仅仅是注释,还是一种特殊的声明语句
这种声明的含义:
- 如果类型
a想要成为类簇Eq实例,那么,它必须支持Eq中声明的两个运算符==/=
声明类型是类簇的实例:
instance Eq Bool where
False == False = True
True == True = True
_ == _ = False
-
只有通过
data和newtype声明的类型,才能够成为类簇的实例 -
类簇中声明的缺省实现,可以在实例声明时被覆盖
类簇之间可以存在扩展关系:即,一个类簇在另一个类簇的基础上进行扩展
class (Eq a) => Ord a where
compare :: a -> a -> Ordering
(<), (<=), (>), (>=) :: a -> a -> Bool
max, min :: a -> a -> a
compare x y = if x == y then EQ
-- NB: must be '<=' not '<' to validate the
-- claim about the minimal things that
-- can be defined for an instance of Ord:
else if x <= y then LT
else GT
x <= y = case compare x y of { GT -> False; _ -> True }
x >= y = y <= x
x > y = not (x <= y)
x < y = not (y <= x)
-- These two default methods use '<=' rather than 'compare'
-- because the latter is often more expensive
max x y = if x <= y then y else x
min x y = if x <= y then x else y
{-# MINIMAL compare | (<=) #-}
data Ordering = LT | EQ | GT
instance Ord Bool where
False <= _ = True
True <= True = True
_ <= _ = False
声明自动成为内置类簇的实例
在定义一个新的类型时,可以通过 deriving 声明,将该类型自动成为指定内置类簇的实例。
data Bool = False | True deriving (Eq, Ord, Show, Read)
ghci> False < True
True
ghci> False == True
False
小和尚:
- 这样太帅了吧!
唐僧:
注意到
deriving声明的限制:它只适用于标准库内置的类簇,不适用于自定义的类簇编译器在背后帮我们生成了所需的代码
07 示例:重言检查器 / Tautology Checker
目标问题:
- 设计一个算法,检查一个 命题公式 (Propositional Formula) 是否总是为真。
以下是 4 个命题公式的示例:
-
A ∧ ¬A -
(A ∧ B) => A -
A => (A ∧ B) -
(A ∧ (A => B)) => B
求解方法: 查看命题公式的真值表,判断是否所有结果都为真
以下是三个操作 (not, and, imply) 对应的真值表:
|
|
|
下面,我们依次列出上面四个命题公式对应的真值表:
| A | ¬A | A ∧ ¬A |
|---|---|---|
| F | T | F |
| T | F | F |
| A | B | (A ∧ B) => A |
|---|---|---|
| F | F | T |
| F | T | T |
| T | F | T |
| T | T | T |
| A | B | A => (A ∧ B) |
|---|---|---|
| F | F | T |
| F | T | T |
| T | F | F |
| T | T | T |
| A | B | (A ∧ (A => B)) => B |
|---|---|---|
| F | F | T |
| F | T | T |
| T | F | T |
| T | T | T |
可以看到,在上面四个命题公式中,有两个重言式:(A ∧ B) => A,(A ∧ (A => B)) => B
下面,我们给出重言式检查算法的设计过程:
第一步: 定义一个用于表示命题公式的类型
data Prop = Cst Bool
| Var Char
| Not Prop
| And Prop Prop
| Imply Prop Prop
则,上述四个命题公式可以表示为:
-- 1. A ∧ ¬A
p1 = And (Var 'A') (Not (Var 'A'))
-- 2. (A ∧ B) => A
p2 = Imply (And (Var 'A') (Var 'B')) (Var 'A')
-- 3. A => (A ∧ B)
p3 = Imply (Var 'A') (And (Var 'A') (Var 'B'))
-- 4. (A ∧ (A => B)) => B
p4 = Imply (And (Var 'A') (Imply (Var 'A') (Var 'B'))) (Var 'B')
第二步: 定义函数 vars :: Prop -> [Char],计算一个命题公式中的变量
vars :: Prop -> [Char]
vars (Cst _) = []
vars (Var x) = [x]
vars (Not p) = vars p
vars (And p q) = vars p ++ vars q
vars (Imply p q) = vars p ++ vars q
ghci> var p4
"AABB"
第三步: 定义一个类型,用于表达命题变量 与 真-假值 之间的 绑定/置换 关系
type Assoc k v = [(k, v)]
type Subst = Assoc Char Bool
-- example
subst :: Subset
subst = [ ('A' ,True), ('B', False) ]
第四步: 定义函数 bools :: Int -> [[Bool]],用于生成 n 个 Bool 值所有可能的排列
bools :: Int -> [[Bool]]
bools 0 = [[]]
bools n = map (False :) bss ++ map (True :) bss
where bss = bools $ n - 1
ghci> bools 2
[[False,False],[False,True],[True,False],[True,True]]
第五步: 定义函数 varSubsts :: [Char] -> [Subst];
- 该函数接收一组命题变量,生成对这些变量所有可能的赋值/置换方式
varSubsts :: [Char] -> [Subst]
varSubsts vs = map (zip vs) (bools $ length vs)
ghci> varSubsts "AB"
[ [('A',False),('B',False)],
[('A',False),('B',True)],
[('A',True),('B',False)],
[('A',True),('B',True)] ]
第六步: 定义函数 eval :: Subst -> Prop -> Bool
- 该函数接收一个置换表和一个命题公式,评估这个命题公式的值
eval :: Subst -> Prop -> Bool
eval _ (Cst b) = b
eval s (Var x) = find x s
eval s (Not p) = not (eval s p)
eval s (And p q) = eval s p && eval s q
eval s (Imply p q) = eval s p <= eval s q
-- ^^ 注意:这里出现了一件很有趣的事情
第七步: 定义函数 isTaut :: Prop -> Bool,判断一个命题公式是否是一个重言式
isTaut :: Prop -> Bool
isTaut p = and [eval s p | s <- varSubsts vs]
where vs = rmdups (vars p)
ghci> isTaut p1
False
ghci> isTaut p2
True
ghci> isTaut p3
False
ghci> isTaut p4
True
08 示例:抽象机器 / Abstract Machine
我们可以定义一个表示 “算术运算表达式” 的类型,然后定义一个评估函数,对一个表达式进行求值:
data Expr = Val Int | Add Expr Expr
value :: Expr -> Int
value (Val n) = n
value (Add x y) = value x + value y
例如,对于表达式 (2 + 3) + 4,其求值过程如下:
value (Add (Add (Val 2) (Val 3)) (Val 4))
=== { applying value }
value (Add (Val 2) (Val 3)) + value (Val 4)
=== { applying the first value }
(value (Val 2) + value (Val 3)) + value (Val 4)
=== { applying the first value}
(2 + value (Val 3)) + value (Val 4)
=== { applying the first value}
(2 + 3) + value (Val 4)
=== { applying the first + }
5 + value (Val 4)
=== { applying value }
5 + 4
=== { applying + }
9
注意:
-
在类型声明中,我们并未指定表达式求值的详细步骤
-
Haskell 编译器在背后帮我们做了很多的事情
一个问题: 可以自定义表达式的求值步骤吗?
下面是一个解决方案:
data Expr = Val Int | Add Expr Expr
value :: Expr -> Int
value e = eval e []
data Op = EVAL Expr | ADD Int -- 两种操作
type Cont = [Op] -- 操作序列
eval :: Expr -> Cont -> Int
eval (Add x y) c = eval x $ EVAL y : c
-- 把对表达式 Add x y 的评估拆成两个部分: eval x 和 EVAL y。后者放入操作序列的头部
eval (Val n ) c = exec c n
exec :: Cont -> Int -> Int
exec [] n = n
exec (EVAL y : c) n = eval y $ ADD n : c
exec (ADD n : c) m = exec c $ n + m
对于表达式 (2 + 3) + 4,其求值过程如下:
value (Add (Add (Val 2) (Val 3)) (Val 4))
=== eval (Add (Add (Val 2) (Val 3)) (Val 4)) []
=== eval (Add (Val 2) (Val 3)) [EVAL (Val 4)]
=== eval (Val 2) [EVAL (Val 3), EVAL (Val 4)]
=== exec [EVAL (Val 3), EVAL (Val 4)] 2
=== eval (Val 3) [ADD 2, EVAL (Val 4)]
=== exec [ADD 2, EVAL (Val 4)] 3
=== exec [EVAL (Val 4)] (2 + 3)
=== eval (Val 4) [ADD (2 + 3)]
=== exec [ADD (2 + 3)] 4
=== exec [] (2 + 3) + 4
=== (2 + 3) + 4
本章作业
作业 01
使用递归和函数
add :: Nat -> Nat -> Nat,定义自然数Nat上的乘法运算
作业 02
给出函数
folde的完整定义,并给出该函数的若干使用案例
作业 03
定一个二叉树类型
Tree a,其中:
叶节点的 Constructor 名为
Leaf,它构造出只包含一个a类型值的二叉树非叶节点的 Constructor 名为
Node,它构造出一个包含两个二叉树的二叉树
第 10 章:案例 Countdown 问题
01 什么是 Countdown 问题
Countdown 问题是一个始于 1982 年的英国电视节目,其中包含了一个关于数字的游戏。
Countdown 问题的一个示例:
请使用如下数字:
137102550以及如下四个运算:
+-×÷构造出一个算术运算表达式,满足表达式的值为
765
Countdown 问题需要满足两条规则:
-
所有的候选数字以及表达式求值过程的中间结果,都必须是正整数
-
所有的候选数字在构造出的表达式中,最多只能出现一次
对于上面的这个示例问题:
137102550=>765
一个解是:
(25 - 10) * (50 + 1)===765这个问题一共有 780 个解
如果将这个问题的目标数字修改为 831,则该问题无解
02 求解 Countdown 问题
定义一个类型 Op,表示四种运算:
data Op = Add | Sub | Mul | Div deriving (Show)
定义函数 apply:该函数将一个运算应用到两个正整数上,返回运算结果:
apply :: Op -> Int -> Int -> Int
apply Add x y = x + y
apply Sub x y = x - y
apply Mul x y = x * y
apply Div x y = x `div` y
定义函数 valid,判断 “将一个操作作用到两个正整数上,其结果是否仍然是一个正整数”:
valid :: Op -> Int -> Int -> Bool
valid Add _ _ = True
valid Sub x y = x > y
valid Mul _ _ = True
valid Div x y = x `mod` y == 0
定义一个类型 Expr,用于表示算术运算表达式:
data Expr = Val Int | App Op Expr Expr deriving (Show)
定义函数 eval,用于评估表达式的值:
eval :: Expr -> [Int]
eval (Val n ) = [ n | n > 0 ]
eval (App o l r) = [ apply o x y | x <- eval l, y <- eval r, valid o x y]
该函数的返回值有如下特点:
-
若表达式的值为一个正整数,则返回一个仅包含该正整数的 list
-
否则,返回一个 empty list
定义若干组合函数:
计算一个 list 的所有 sub-list:
subs :: [a] -> [[a]]
subs [] = [[]]
subs (x:xs) = let yss = subs xs in yss ++ map (x:) yss
ghci> subs [1, 2, 3]
[ [], [3], [2], [2, 3], [1], [1, 3], [1, 2], [1, 2, 3] ]
- 注意:这里的 sub-list 不会改变元素之间的相对位置
=== subs (3:[])
=== subs [] ++ map (3:) (subs [])
=== [[]] ++ map (3:) [[]]
=== [[]] ++ [[3]]
=== [[],[3]]
subs (2:3:[])
=== subs (3:[]) ++ map (2:) (subs (3: []))
=== [[],[3]] ++ map (2:) [[],[3]]
=== [[],[3]] ++ [[2], [2,3]]
=== [[],[3],[2],[2,3]]
subs [1, 2, 3]
=== subs (1:2:3:[])
=== subs (2:3:[]) ++ map (1:) (subs (2:3:[]))
=== [[],[3],[2],[2,3]] ++ map (1:) [[],[3],[2],[2,3]]
=== [[],[3],[2],[2,3]] ++ [[1],[1,3],[1,2],[1,2,3]]
=== [[],[3],[2],[2,3],[1],[1,3],[1,2],[1,2,3]]
计算将一个元素插入一个 list 中的所有可能方式:
interleave :: a -> [a] -> [[a]]
interleave x [] = [[x]]
interleave x (y:ys) = (x:y:ys) : map (y:) (interleave x ys)
ghci> interleave 1 [2, 3, 4]
[ [1,2,3,4], [2,1,3,4], [2,3,1,4], [2,3,4,1] ]
计算一个 list 中全部元素的所有可能排列 (Permutation):
perms :: [a] -> [[a]]
perms [] = [[]]
perms (x:xs) = concat $ map (interleave x) (perms xs)
ghci> perms [1, 2, 3]
[ [1,2,3], [2,1,3], [2,3,1], [1,3,2], [3,1,2], [3,2,1] ]
计算对一个 list 中的零或多个元素的所有可能选择方式:
choices :: [a] -> [[a]]
choices = concat . map perms . subs
ghci> choices [1, 2, 3]
[ [], [3], [2], [2,3], [3,2], [1], [1,3], [3,1], [1,2], [2,1],
[1,2,3], [2,1,3], [2,3,1], [1,3,2], [3,1,2], [3,2,1] ]
03 形式化 Countdown 问题
计算一个表达式中出现的所有值:
values :: Expr -> [Int]
values (Val n ) = [n]
values (App _ l r) = values l ++ values r
判断一个表达式是否是一个 Countdown 问题的解:
solution :: Expr -> [Int] -> Int -> Bool
solution e ns n = (values e) `elem` (choices ns) && eval e == [n]
04 暴力搜索方法
计算将一个 list 分裂为两个非空 list 的所有可能方式:
split :: [a] -> [([a],[a])]
split [] = []
split [_] = []
split (x:xs) = ([x],xs) : [ (x:ls, rs) | (ls,rs) <- split xs ]
ghci> split [1, 2, 3, 4]
[ ([1], [2,3,4]), ([1,2], [3,4]), ([1,2,3], [4]) ]
计算所有满足如下条件的表达式:
- 该表达式中包含的值恰好是一个给定的
[Int]
exprs :: [Int] -> [Expr]
exprs [] = [] -- 给定的 [Int] 为空
exprs [n] = [Val n] -- 给定的 [Int] 只包含一个整数值
exprs ns = [e | (ls,rs) <- split ns
, l <- exprs ls
, r <- exprs rs
, e <- combine l r]
combine :: Expr -> Expr -> [Expr]
combine l r = [ App o l r | o <- [Add, Sub, Mul, Div] ]
计算一个 Countdown 问题的所有解:
solutions :: [Int] -> Int -> [Expr]
solutions ns n = [ e | ns' <- choices ns
, e <- exprs ns'
, eval e == [n] ]
这种方法的效率
| Hardware | 2.8GHz Core 2 Duo, 4GB RAM |
| Compiler | GHC version 7.10.2 |
| Example | solutions [1,3,7,10,25,50] 765 |
| One solution | 0.108 seconds |
| All solutions | 12.224 seconds |
继续改进
大部分我们考察的表达式都是不合法的 (对这些不合法的表达式进行评估,总是返回一个 empty list):
- 上面的这个 Countdown 问题,总计约 3300 万个表达式,但只有约 500 万个表达式合法
因此,将表达式的生成和评估融合在一起,会尽早发现并拒绝不合法的表达式,从而提高效率。
05 融合表达式的生成与评估
定义一个类型 Result,用于记录合法的表达式以及评估结果:
type Result = (Expr, Int)
定义一个函数 results,计算包含给定值序列的合法表达式及其评估结果:
-
生成与评估相互独立的
results函数:results :: [Int] -> [Result] results ns = [ (e,n) | e <- exprs ns, n <- eval e ] -
生成与评估相融合的
results函数results :: [Int] -> [Result] results [] = [] results [n] = [(Val n, n) | n > 0] results ns = [ res | (ls,rs) <- split ns , lx <- results ls , ry <- results rs , res <- combine' lx ry ] combine' :: Result -> Result -> [Result] combine' (l,x) (r,y) = [ (App o l r, apply o x y) | o <- [Add,Sub,Mul,Div] , valid o x y]
一个更好的计算方法:
solutions' :: [Int] -> Int -> [Expr]
solutions' ns n = [ e | ns' <- choices ns, (e,m) <- results ns', m == n ]
这种方法的效率
| Hardware | 2.8GHz Core 2 Duo, 4GB RAM | ||
| Compiler | GHC version 7.10.2 | ||
| Example | solutions [1,3,7,10,25,50] 765 | ||
| One solution | 0.108 s | 0.014 s | |
| All solutions | 12.224 s | 1.312 s | |
| 暴力搜索 | 融合生成与评估 | ||
继续改进
很多表达式实际上是相互等价的,例如:
x * y==y * xx * 1==x
减少对这些等价表达式的搜索,可以进一步提交效率
06 改进 valid 函数
valid :: Op -> Int -> Int -> Bool
valid Add x y = x <= y
valid Sub x y = x > y
valid Mul x y = x <= y && x /= 1 && y /= 1
valid Div x y = x `mod` y == 0 && y /= 1
-- 原来的版本
valid :: Op -> Int -> Int -> Bool
valid Add x y = True
valid Sub x y = x > y
valid Mul x y = True
valid Div x y = x `mod` y == 0
这种方法的效率
| Hardware | 2.8GHz Core 2 Duo, 4GB RAM | ||
| Compiler | GHC version 7.10.2 | ||
| Example | solutions [1,3,7,10,25,50] 765 | ||
| One solution | 0.108 s | 0.014 s | 0.007 s |
| All solutions | 12.224 s | 1.312 s | 0.119 s |
| 暴力搜索 | 融合生成与评估 | 改进的 valid | |
本章作业
作业 01
修改最终版本的 Countdown 问题计算方法,实现如下功能增强:
允许在表达式中存在指数运算
如果找不到精确解,则生成所有距离精确解最近的解 (Nearest Solutions)
确定一种对解的简洁性进行评估的指标,然后对生成的解按照这个指标进行排序
第 11 章:交互式程序设计
01 交互式程序
到目前为止,我们接触到的绝大多数 Haskell 程序都可以归为 批处理程序 (Batch Program)。
批处理程序是这样一种程序:
-
它在开始时接收一组参数,然后在结束时返回一个值
- 在执行过程中 (即,开始与结束之间),该程序无法接收外部的参数,也不会向外界输出信息

与批处理程序相对的,是 交互式程序 (Interactive Program):这类程序在执行过程中能够从键盘读入信息,并向屏幕输出信息。
令人遗憾的是,在 Haskell 中编写交互式程序,是一件相对困难的事情。
-
Haskell 程序在本质上是数学意义上的 纯函数 (Pure Function)。
-
从来没有一本数学书或一位数学家说:一个函数可以与键盘或屏幕这种世俗的东西发生交互
-
也即,数学中的函数没有 副作用 (Side Effects):即,不会对世界的状态产生直接的改变
-
-
但是,交互式程序具有副作用:即,从键盘读入信息、向屏幕输出信息
但是,一件 非常搞笑 的事情是:
- 只要把我们的思维方式稍微调整一下,Haskell 无法处理交互式程序的问题就迎刃而解了
任何一个交互式程序都可以为被视为一个纯函数:
-
该函数的输入参数:世界的当前状态 (The current state of the world)
-
该函数的输出参数:改变后的世界 (A modified world)
type IO = WORLD -> WORLD
为了将计算结果进行显式化,可以对上述类型定义进行轻微调整:
type IO a = WORLD -> (a, WORLD)
因此,Haskell 中的交互式程序,具有 IO a 这种类型:
- 称这种类型的一个值,是一个返回一个
a类型值的 动作 (Action)
唐僧:
- 你不会真的以为,
IO a把整个世界的状态读入程序吧?小和尚:
- 如果你不说,我们还真这样认为呢 (看,我们多天真🐯)
02 Prelude 模块提供的若干 IO 动作
getChar :: IO Char
该动作具有如下行为:
-
读入用户通过键盘输入的一个字符
-
将这个字符输出到屏幕上
-
将这个字符作为返回值
putChar :: Char -> IO ()
该函数具有如下行为:
-
接收一个字符
c作为输入参数 -
返回一个动作:该动作向屏幕输出字符
c,并返回一个零元组()
return :: a -> IO a
该函数具有如下行为:
-
接收一个
a类型的参数x -
返回一个动作:该动作不产生任何副作用,直接返回
x
注意:千万不要把这个
return函数与其他语言中的return关键字混淆了
Haskell 提供了一个关键字
do,用于表达 “顺序执行若干动作”。例如:
act :: IO (Char, Char) act = do x <- getChar getChar y <- getChar return (x, y)
首先注意到,这个动作的类型是
IO (Char, Char)
- 也即,在执行完动作后,会返回一个类型为
(Char, Char)的值
do后面顺序放置了 4 个 动作
x <- getChar
执行动作
getChar,并把返回的那个Char值赋到变量x上注意:
getChar的类型是IO Char因此,
x = getChar这种方式无法把IO Char中的Char赋给x这里的
<-,就是 List Comprehension 中的 Generator 中的<-
- 更多细节,在后文中讲解
getChar
- 执行
getChar这个动作,且忽略其返回值
y <- getChar
- 执行动作
getChar,并把返回的那个Char值赋到变量x上
return (x, y)
return的类型:a -> IO a
从键盘读入一行字符串:
getLine :: IO String
getLine = do x <- getChar
if x == '\n' then
return []
else
do xs <- getLine
return (x:xs)
向屏幕输出一个字符串:
putStr :: String -> IO ()
putStr [] = return ()
putStr (x:xs) = do putChar x
putStr xs
向屏幕输出一个字符串,并换行:
putStrLn :: String -> IO ()
putStrLn xs = do putStr xs
putChar '\n'
一个简单的交互式程序
strlen :: IO ()
strlen = do putStr "Enter a string: "
xs <- getLine
putStr "The string has "
putStr (show (length xs))
putStrLn " characters"
ghci> strlen
Enter a string: Haskell
The string has 7 characters
03 示例:Hangman 游戏
游戏规则:
-
玩家一:在键盘上秘密地输入一个单词
secret -
玩家二:尝试去推理出这个单词。推理过程如下:
-
玩家二在键盘上输入一个猜测的单词
guess -
计算机点亮
secret中那些出现在guess中的字母 -
玩家二跳转到第 1 步,进行新一轮的猜测,直到猜中
-
ghci> hangman
Think of a word:
-------
Try to guess it:
? pascal
-as--ll
? rust
--s----
? haspell
has-ell
? haskell
You got it!
下面,我们采用自顶向下的策略实现这个游戏。
首先给出最顶层的函数:
hangman :: IO ()
hangman = do
putStrLn "Think of a word: "
word <- sgetLine -- get a string secretly
putStrLn "Try to guess it:"
play word -- play the game
其中,动作 sgetLine 的行为:
-
从键盘上读入一行字符串
secret -
将其中的每一字母以字符
-输出到屏幕
sgetLine :: IO String
sgetLine = do
x <- getCh -- get a char without echoing
if x == '\n' then
do putChar x
return []
else
do putChar '-'
xs <- sgetLine
return (x:xs)
其中,动作 getCh 的行为:
- 从键盘读入一个字符,但是不把这个字符输出到屏幕
import System.IO (hSetEcho, stdin)
getCh :: IO Char
getCh = do
hSetEcho stdin False
x <- getChar
hSetEcho stdin True
return x
- 这里有一些底层的实现细节,可以不用太关注
函数 play 是游戏的主体:支持玩家二不断进行猜测,并输出系统的反馈。
play :: String -> IO ()
play word = do
putStr "? "
guess <- getLine
if guess == word then
putStrLn "You got it!"
else
do putStrLn (match word guess)
play word
match :: String -> String -> String
match xs ys = [if elem x ys then x else '-' | x <- xs]
04 示例:Nim 游戏
游戏规则:
-
一个棋盘,初始状态如下:
1: * * * * * 2: * * * * 3: * * * 4: * * 5: * -
两个玩家轮流对棋盘进行如下操作:
- 选择一行,并从这一行的尾部删除一或多个
*
- 选择一行,并从这一行的尾部删除一或多个
-
清空棋盘的玩家是游戏的赢家
下面,我们采用自底向上的策略实现这个游戏。
棋盘的表示和显示:
type Board = [Int]
initial :: Board
initial = [5,4,3,2,1]
finished :: Board -> Bool
finished = all (== 0)
putBoard :: Board -> IO ()
putBoard [a, b, c, d, e] = do
putRow 1 a
putRow 2 b
putRow 3 c
putRow 4 d
putRow 5 e
putRow :: Int -> Int -> IO ()
putRow row num = do
putStr $ show row
putStr ": "
putStrLn $ concat $ replicate num "* "
ghci> putBoard initial
1: * * * * *
2: * * * *
3: * * *
4: * *
5: *
游戏中的一次操作:从一行的尾部删除一或多个 *
-- 判断一次操作是否合法
valid :: Board -> Int -> Int -> Bool
valid board row del = board !! (row - 1) >= del
-- (!!) :: [a] -> Int -> a
-- List index (subscript) operator, starting from 0
-- (exported by Prelude)
-- 进行一次操作
move :: Board -> Int -> Int -> Board
move board row del = [ update r n | (r,n) <- zip [1..] board ]
where
update r n = if r == row then n - del else n
游戏主函数:
nim :: IO
nim = play initial 1
play :: Board -> Int -> IO ()
play board player =
do newline
putBoard board
newline
if finished board then
do putStr "Player "
putStr $ show $ next player
putStrLn " wins!!"
else
do putStr "Player "
putStrLn $ show player
row <- getDigit "Enter a row number: "
del <- getDigit "Stars to remove: "
if valid board row del then
play (move board row del) (next player)
else
do newline
putStrLn "ERROR: Invalid move"
play board player
本章作业
作业 01
定义一个动作
adder :: IO (),它具有如下行为:
- 从键盘读入一个正整数
n- 从键盘读入
n个整数 (每个整数一行),然后输出这n个整数的和例如:
ghci> adder How many numbers? 5 1 3 5 7 9 The total is 25
第 12 章:Monad and More
主要知识点:
Functor|Applicative|Monad
01 提升代码抽象层次的两种方式
方式一: 对类型进行抽象 => 多态函数 (Polymorphic Function)
例如:
length1 :: [a] -> Int
a是一个类型变量
方式二: 对 Type Constructor 进行抽象 => 范型函数 (Generic Function)
例如:
length2 :: t a -> Int
t是一个表示 Type Constructor 的变量
02 Functor (函子)
计算的抽象
|
|
上述两个函数中的共性成分可以被表示为一个高阶函数:
map :: (a -> b) -> [a] -> [b]
map f [] = []
map f (x:xs) = f x : map f xs
在此基础上,上述两个函数可以被改写为:
|
|
注意到:
-
在 Haskell 中,类型
[a]也可以被写为[] a。 -
也即:
[]是一个 Type Constructor- 它接收一个类型作为参数,返回/构造一个新的类型
可以将
[]的类型 “理解为”Type -> Type- 注意:
Type不是 Haskell 中的一个类型;因此,仅仅是 “理解为”
更严格而言,应该用如下方式理解
[]ctor [] :: Type -> Type
Functor 的目的:
- 把适用于
[]的map函数推广到任何一个与[]具有相同类型的 Type Constructor
Functor 的定义
-- Exported by Prelude
class Functor f where
fmap :: (a -> b) -> f a -> f b
(<$) :: b -> f a -> f b
(<$) = fmap . const
const :: b -> a -> b
const x _ = x
-
f:一个表示 Type Constructor 的变量-
不是所有的 Type Constructor 都可以被
f抽象 -
只有类型为
Type -> Type的 Type Constructor 才可以被f抽象 -
“
f只能具有一个参数” 的限制,在fmap的类型中可以被观察到
-
-
如果你看不懂
<$的定义,我们再捋一捋x <$ y === (fmap . const) x y === fmap (const x) y === fmap (\_ -> x) y
把 Type Constructor 声明为 Functor 的实例
-- Exported by Prelude
instance Functor [] where
fmap :: (a -> b) -> [a] -> [b]
fmap = map
ghci> fmap (+1) [1, 2, 3]
[2, 3, 4]
ghci> fmap (^2) [1, 2, 3]
[1, 4, 9]
data Maybe a = Nothing | Just a
instance Functor Maybe where
fmap :: (a -> b) -> Maybe a -> Maybe b
fmap _ Nothing = Nothing
fmap g (Just x) = Just $ g x
ghci> fmap (+1) (Just 3)
Just 4
ghci> fmap (+1) Nothing
Nothing
ghci> fmap not (Just False)
Just True
data Tree a = Leaf a | Node (Tree a) (Tree a) deriving (Show)
instance Functor Tree where
fmap :: (a -> b) -> Tree a -> Tree b
fmap g (Leaf x) = Leaf $ g x
fmap g (Node l r) = Node (fmap g l) (fmap g r)
ghci> fmap length $ Leaf "abc"
Leaf 3
ghci> fmap even $ Node (Leaf 1) (Leaf 2)
Node (Leaf False) (Leaf True)
instance Functor IO where
fmap :: (a -> b) -> IO a -> IO b
fmap g mx = do
x <- mx
return $ g x
ghci> fmap show $ return True
"True"
定义 Generic Function
inc :: Functor f => f Int -> f Int
inc = fmap (+1)
ghci> inc $ Just 1
Just 2
ghci> inc [1,2,3,4,5]
[2,3,4,5,6]
ghci> inc $ Node (Leaf 1) (Leaf 2)
Node (Leaf 2) (Leaf 3)
Functor Laws
任何一个 Functor 的实例,都必须满足如下两个性质:
-
fmap id===id -
fmap (f . g)===fmap f . fmap g
在 Haskell 中,任何一个类型为
Type -> Type的 Type Constructor,最多只有一个满足上述性质fmap函数
- 也即,如果一个 Type Constructor 能够成为 Functor 的实例,那么,只有唯一一种实现方式
唐僧:
如果你想要知道 “为什么要求上述命题成立”,那么,我只能忽悠你去学习 “范畴论”
- 如果你面临物质上的压力,那最好还是放弃;因为,目前看来,不是热点,赚不到钱
暂时不要尝试去理解 Functor Laws 的本质
- 在没有学习过 “范畴论” 的情况下,所有的理解大概都可以归类为 “盲人摸象”
fmap 对应的运算符
-- Exported by Prelude
(<$>) :: Functor f => (a -> b) -> f a -> f b
(<$>) = fmap
- 运算符
<$>可以类比到运算符$($) :: (a -> b) -> a -> b (<$>) :: Functor f => (a -> b) -> f a -> f b
03 Applicative Functor (简称为 Applicative)
如何定义一个一般性的 fmap
fmap0 :: a -> f a
fmap1 :: (a -> b) -> f a -> f b
fmap2 :: (a -> b -> c) -> f a -> f b -> f c
fmap3 :: (a -> b -> c -> d) -> f a -> f b -> f c -> f d
...
两个基本函数
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
在这两个函数的基础上,就可以定义任何一个一般性的 fmap
fmap0 :: a -> f a
fmap0 = pure
fmap1 :: (a -> b) -> f a -> f b
fmap1 g x = pure g <*> x
-- 或者
fmap1 g x = fmap g x = g <$> x
fmap2 :: (a -> b -> c) -> f a -> f b -> f c
fmap2 g x y = pure g <*> x <*> y = g <$> x <*> y
fmap3 :: (a -> b -> c -> d) -> f a -> f b -> fc -> f d
fmap3 g x y z = pure g <*> x <*> y <*> z = g <$> x <*> y <*> z
Applicative 的定义 (一个简化版本)
class Functor f => Applicative f where
-- Lift a value
pure :: a -> f a
-- Sequential application.
(<*>) :: f (a -> b) -> f a -> f b
把 Type Constructor 声明为 Applicative 的实例
instance Applicative Maybe where
pure :: a -> Maybe a
pure = Just
(<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
Nothing <*> _ = Nothing
(Just g) <*> mx = g <$> mx
ghci> pure (+1) <*> Just 1
Just 2
ghci> pure (+) <*> Just 1 <*> Just 2
Just 3
ghci> pure (+) <*> Nothing <*> Just 2
Nothing
ghci> Nothing <*> Just 1
Nothing
instance Applicative [] where
pure :: a -> [a]
pure x = [x]
(<*>) :: [a -> b] -> [a] -> [b]
gs <*> xs = [g x | g <- gs, x <- xs]
ghci> pure (+1) <*> [1,2,3]
[2,3,4]
ghci> pure (+) <*> [1] <*> [2]
[3]
ghci> pure (*) <*> [1,2] <*> [3,4]
[3,4,6,8]
instance Applicative IO where
pure :: a -> IO a
pure = return
(<*>) :: IO (a -> b) -> IO a -> IO b
mg <*> mx = do { g <- mg; x <- mx; return (g x) }
getChars :: Int -> IO String
getChars 0 = return []
getChars n = pure (:) <*> getChar <*> getChars (n-1)
定义 Generic Function
sequenceA :: Applicative f => [f a] -> f [a]
sequenceA [] = pure []
sequenceA (x:xs) = pure (:) <*> x <*> sequenceA xs
ghci> sequenceA [Just 1, Just 2, Just 3]
Just [1,2,3]
sequenceA [Just 1, Just 2, Just 3]
=== sequenceA ((Just 1):[Just 2, Just 3])
=== pure (:) <*> Just 1 <*> sequenceA [Just 2, Just 3]
=== Just (:) <*> Just 1 <*> sequenceA [Just 2, Just 3]
=== Just (1:) <*> sequenceA [Just 2, Just 3]
=== Just (1:) <*> sequenceA ((Just 2):[Just 3])
=== Just (1:) <*> (pure (:) <*> Just 2 <*> sequenceA [Just 3])
=== Just (1:) <*> (Just (2:) <*> sequenceA ((Just 3):[]))
=== Just (1:) <*> (Just (2:) <*> (pure (:) <*> Just 3 <*> sequenceA [])
=== Just (1:) <*> (Just (2:) <*> (Just (3:) <*> sequenceA [])
=== Just (1:) <*> (Just (2:) <*> (Just (3:) <*> pure [])
=== Just (1:) <*> (Just (2:) <*> (Just (3:) <*> Just [])
=== Just (1:) <*> (Just (2:) <*> (Just (3:[]))
=== Just (1:) <*> (Just (2:3:[]))
=== Just (1:2:3:[])
=== Just [1, 2, 3]
ghci> sequenceA [Just 1, Nothing, Just 3]
Nothing
sequenceA [Just 1, Nothing, Just 3]
=== sequenceA (Just 1):[Nothing, Just 3]
=== pure (:) <*> Just 1 <*> sequenceA [Nothing, Just 3]
=== pure (1:) <*> sequenceA (Nothing:[Just 3])
=== pure (1:) <*> (pure (:) <*> Nothing <*> sequenceA [Just 3])
=== pure (1:) <*> (Just (:) <*> Nothing <*> sequenceA [Just 3])
=== pure (1:) <*> ( (:) <$> Nothing <*> sequenceA [Just 3])
=== pure (1:) <*> ( Nothing <*> sequenceA [Just 3])
=== pure (1:) <*> ( Nothing)
=== Just (1:) <*> Nothing
=== (1:) <$> Nothing
=== Nothing
唐僧:
- 当
sequenceA :: Applicative f => [f a] -> f [a]中的f是Maybe时,- 你能观察到
sequenceA的效果吗?小和尚:
- 观察不到;愿闻其详
唐僧:
把
Maybe视为一种可能存在失败的计算活动
- 当失败时,返回
Nothing;当成功时,返回Just _把
sequenceA [x, y, z]视为顺序执行一组可能存在失败的计算活动x, y, z
若在执行一个计算活动时发生失败,则终止后续的计算活动,直接返回
Nothing否则,将所有计算结果存储为序列
rsts = [r1, r2, r3],并返回Just rsts小和尚:
- 这种效果是刻意设计出来的吗?
唐僧:
感觉不是
更像是背后的数学结构天然具有的性质
如同我们所生活的物理空间天然存在的物理规律一样
我们只是观察者,而不是设计者
ghci> sequenceA [[1,2,3], [4,5,6], [7,8,9]]
[[1,4,7],[1,4,8],[1,4,9],[1,5,7],[1,5,8],[1,5,9],[1,6,7],[1,6,8],[1,6,9],
[2,4,7],[2,4,8],[2,4,9],[2,5,7],[2,5,8],[2,5,9],[2,6,7],[2,6,8],[2,6,9],
[3,4,7],[3,4,8],[3,4,9],[3,5,7],[3,5,8],[3,5,9],[3,6,7],[3,6,8],[3,6,9]]
唐僧:
- 当
sequenceA :: Applicative f => [f a] -> f [a]中的f是[]时,- 你能观察到
sequenceA的效果吗?小和尚:
- 我观察到了;非常感谢 🤝
Applicative Laws
任何一个 Applicative Functor 的实例,都必须满足如下性质:
如上所述,暂时不要去理解这些 Laws 的本质
- 但不妨碍我们做一点简单的类型分析
-
pure id <*> x===x-
若
id :: a -> a,则x :: f a记当前的 Applicative 实例为
f(下同)
-
-
pure (g x)===pure g <*> pure x- 若
x :: a,则g :: a -> b,pure (g x) :: f b
- 若
-
x <*> pure y===pure (\g -> g y) <*> x- 若
y :: a,则x :: f (a -> b),pure (\g -> g y) :: f ((a -> b) -> b)
- 若
-
x <*> (y <*> z)===(pure (.) <*> x <*> y) <*> z-
若
z :: f a,则y :: f (a -> b),x :: f (b -> c), -
且
pure (.) <*> x <*> y :: f (a -> c)
-
04 Monad
一个小问题:异常处理
data Expr = Val Int | Div Expr Expr
eval :: Expr -> Int
eval (Val n) = n
eval (Div x y) = eval x `div` eval y
ghci> eval $ Div (Val 1) (Val 0)
** Exception: divide by zero
解决方法一 (稍显繁琐)
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv n m = Just (n `div` m)
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) = case eval x of
Nothing -> Nothing
Just n -> case eval y of
Nothing -> Nothing
Just m -> safediv n m
解决方法二 (仍然不够简洁)
先给出一个存在类型错误的版本:
eval :: Expr -> Maybe Int
eval (Val n) = pure n
eval (Div x y) = pure safediv <*> eval x <*> eval y
-- ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-- 类型错误:Maybe (Maybe Int)
改正上面的类型错误:
eval :: Expr -> Maybe Int
eval (Val n) = pure n
eval (Div x y) = case pure safediv <*> eval x <*> eval y of
Just r -> r
Nothing -> Nothing
解决方法三 (引入一个新的操作 bind)
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
mx >>= f = case mx of
Nothing -> Nothing
Just x -> f x
eval :: Expr -> Maybe Int -- Maybe Int
eval (Val n) = Just n -- ∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨∨
eval (Div x y) = eval x >>= (\n -> (eval y >>= (\m -> safediv n m)))
-- ^^^^^^ ^ ^^^^^^ ^ ^^^^^^^^^^^
-- Maybe Int Int Maybe Int Int Maybe Int
可以看到:
- 上面程序的最后一行中的圆括号全部都可以去除 (不会引起歧义)
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) = eval x >>= \n -> eval y >>= \m -> safediv n m
do 到底是什么?
下面,我们通过两步变换,向同学们展示一个非常肤浅的世纪大骗局!
第一步:先耍一些朝三暮四的小把戏
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) = eval x >>= \n ->
eval y >>= \m ->
safediv n m
第二步:再撒一点扑朔迷离的语法糖
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) = do n <- eval x
m <- eval y
safediv n m
唐僧:
- 是的,这就是我们在前面看到的神神秘秘、犹抱琵琶半遮面的
do语法的本质小和尚:
- 这种无聊的形式上的变换,真的适合在大学课堂上讲授吗?
唐僧:
千万不能有这种 “看似深刻、其实肤浅” 的想法哟!
数学上的任何一个定理,何尝又非如此呢!
- 定理的结论,仅仅是前提中信息的一种等价变换,并没有增加任何新的信息
Prelude 中 Monad 的定义
{- The "Monad" class defines the basic operations over a "monad",
a concept from a branch of mathematics known as "category theory".
From the perspective of a Haskell programmer, however,
it is best to think of a monad as an "abstract datatype of actions".
Haskell's "do" provide a convenient syntax for writing monadic expressions.
-}
class Applicative m => Monad m where
-- Sequentially compose two actions, passing any value produced
-- by the first as an argument to the second.
(>>=) :: m a -> (a -> m b) -> m b
-- 表达式 ma >>= mb 等价于如下 do 表达式:
-- do a <- ma
-- mb a
-- Sequentially compose two actions, discarding any value produced
-- by the first, like sequencing operators (such as the semicolon)
-- in imperative languages.
(>>) :: m a -> m b -> m b
m >> k = m >>= \_ -> k
-- 表达式 ma >> mb 等价于如下 do 表达式:
-- do ma
-- mb
-- Inject a value into the monadic type.
-- This function should not be different from its default implementation
-- as 'pure'. The justification for the existence of this function is
-- merely historic.
return :: a -> m a
return = pure
把注释删除后,Monad 的定义很简单:
class Applicative m => Monad m where
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
m >> k = m >>= \_ -> k
return :: a -> m a
return = pure
-
Monad 要求实现的三个方法中,两个已经有缺省实现
-
因此,要把一个 Type Constructor 声明为 Monad 的实例,仅需实现方法
(>>=)
把 Type Constructor 声明为 Monad 的实例
instance Monad Maybe where
-- (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
Nothing >>= _ = Nothing
(Just x) >>= f = f x
instance Monad [] where
-- (>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = [y | x <- xs, y <- f x]
05 案例:The State Monad
目标问题:如何用函数描述状态的变化
我们可以将待表达的状态建模为一个 类型。
例如,假如这个状态可以建模为类型 Int,那么,可以将状态表示为如下形式:
type State = Int
注意:
你可以根据实际需求,将任何一种类型作为
State这里将
Int作为State,仅仅是一种举例
然后,状态的变化可以表示为如下类型:
type StateTrans = State -> State
发生状态变化时,有可能会附带一个计算结果。OK,我们把计算结果也表示出来:
type StateTrans a = State -> (a, State)
- 称
StateTrans为 “状态变换器”
如前所述,Haskell 不支持将类型别名 (即,用关键字 type 声明的类型) 声明为类簇的实例。
OK, 我们来主动适应你:用 newtype 重新定义 StateTrans。
newtype StateTrans a = ST (State -> (a, State))
注意:
-
StateTrans是一个 Type Constructor,其类型可以理解为Type -> Type- 因此,有可能将
StateTrans声明为FunctorApplicativeMonad的实例
- 因此,有可能将
-
ST是一个 Data Constructor,其类型为(State -> (a, State)) -> StateTrans a
然后,我们可以定义一个函数 app:将一个状态变换器应用到一个状态上。
app :: StateTrans a -> State -> (a, State)
app (ST f) s = f s
或者更简洁:
app :: StateTrans a -> State -> (a, State)
app (ST f) = f
看起来,把
app命名为unwrap也挺好的
将 StateTrans 声明为 Functor 的实例
instance Functor StateTrans where
-- fmap :: (a -> b) -> StateTrans a -> StateTrans b
fmap g st = ST $ \s -> let (x, s') = app st s in (g x, s')
┌──────────────────────────────────────────────┐
│ fmap g st :: StateTrans b │
│ ┌────────────────────┐ ┌─────┐ │
│ │ │==> x ====>│ g │==>│==> g x
│ │ st :: StateTrans a │ └─────┘ │
s ==>│==>│ │==> s' =============>│==> s'
│ └────────────────────┘ │
└──────────────────────────────────────────────┘
将 StateTrans 声明为 Applicative 的实例
instance Applicative ST where
-- pure :: a -> StateTrans a
pure x = ST $ \s -> (x, s)
-- (<*>) :: StateTrans (a -> b) -> StateTrans a -> StateTrans b
stf <*> stx = ST $ \s -> let (f, s' ) = app stf s
(x, s'') = app stx s'
in (f x, s'')
┌──────────────────────────┐
│ │==> x
│ pure x :: StateTrans a │
s ==>│ │==> s
└──────────────────────────┘
┌────────────────────────────────────────────────────┐
│ stf <*> stx :: StateTrans b │
│ ┌───────┐ ┌─────┐ │
│ │ │==> f =======================>│ │==>│==> f x
│ │ │ ┌───────┐ │ $ │ │
│ │ │ │ │==> x ====>│ │ │
│ │ │ │ │ └─────┘ │
s ==>│==>│ stf │==> s' ==>│ stx │==> s'' ============>│==> s''
│ └───────┘ └───────┘ │
└────────────────────────────────────────────────────┘
将 StateTrans 声明为 Monad 的实例
instance Monad ST where
-- (>>=) :: StateTrans a -> (a -> StateTrans b) -> StateTrans b
st >>= f = ST $ \s -> let (x, s') = app st s
in app (f x) s'
┌────────────────────────────────────────┐
│ st >>= f :: StateTrans b │
│ ┌──────┐ ┌───────┐ │
│ │ │==> x ==>│ f ╞═══╗ │
│ │ │ └───────┘ ⇓ │
│ │ │ ┌───╨───┐ │
│ │ │ │ │==>│==> _ :: b
│ │ │ │ f x │ │
s ==>│==>│ st │==> s' =========>│ │==>│==> _ :: State
│ └──────┘ └───────┘ │
└────────────────────────────────────────┘

06 The State Monad 应用示例:树的重新标注
目标问题
给定如下表示二叉树的一种类型:
data Tree a = Leaf a | Node (Tree a) (Tree a) deriving Show
tree :: Tree Char
tree = Node (Node (Leaf 'a') (Leaf 'b')) (Leaf 'c')
定义一个函数 relabel :: Tree a -> Tree Int:
-
将树中叶子节点中包含的元素映射为一个唯一的整数编号。例如:
ghci> relabel tree Node (Node (Leaf 0) (Leaf 1)) (Leaf 2)
解决方法一:直观朴素法
rlabel :: Tree a -> Int -> (Tree Int, Int)
rlabel (Leaf _ ) n = (Leaf n, n+1)
rlabel (Node l r) n = (Node l' r', n'') where
(l', n' ) = rlabel l n
(r', n'') = rlabel r n'
relabel :: Tree a -> Tree Int
relabel t = fst (rlabel t 0)
缺点:
rlabel的定义中,需要显式维护中间状态
解决方法二:Applicative
fresh :: StateTrans Int
fresh = ST $ \n -> (n, n + 1) -- 将状态从 n 变换为 n + 1, 同时返回计算结果 n
alabel :: Tree a -> StateTrans (Tree Int)
-- :: Int -> Tree Int
-- ↓↓↓↓
alabel (Leaf _) = Leaf <$> fresh
-- ↑↑↑↑↑
-- :: StateTrans Int
-- :: Tree Int -> Tree Int -> Tree Int
-- ┊┊┊┊ :: StateTrans (Tree Int)
-- ┊┊┊┊ ┊┊┊┊┊┊┊┊ :: StateTrans (Tree Int)
-- ↓↓↓↓ ↓↓↓↓↓↓↓↓ ↓↓↓↓↓↓↓↓
alabel (Node l r) = Node <$> alabel l <*> alabel r
-- ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
-- :: StateTrans (Tree Int -> Tree Int)
relabel' :: Tree a -> Tree Int
relabel' t = fst $ app (alabel t) 0
唐僧:
我时常在想,这些东西是永恒的吗?
如果是,那么,它们栖身何处,以至可以被人类发现并表达?
解决方法三:Monad
mlabel :: Tree a -> StateTrans (Tree Int)
-- :: StateTrans Int
-- ┊┊┊┊┊ :: StateTrans (Tree Int)
-- ↓↓↓↓↓ ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
mlabel (Leaf _) = fresh >>= \n -> return $ Leaf n
-- ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
-- :: Int -> StateTrans (Tree Int)
mlabel (Node l r) = mlabel l >>= \l' ->
mlabel r >>= \r' -> return $ Node l' r'
-- ↑↑↑↑↑↑↑↑ ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
-- ┊┊┊┊┊┊┊┊ :: Tree Int -> StateTrans (Tree Int)
-- :: StateTrans (Tree Int)
-- ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
-- :: StateTrans (Tree Int)
relabel'' :: Tree a -> Tree Int
relabel'' t = fst $ app (mlabel t) 0
可以使用 do 语法对 mlabel 进行改写:
mlabel (Leaf _ ) = do n <- fresh
return $ Leaf n
mlabel (Node l r) = do l' <- mlabel l
r' <- mlabel r
return $ Node l' r'
07 Monad Laws
class Applicative m => Monad m where (>>=) :: m a -> (a -> m b) -> m b (>>) :: m a -> m b -> m b m >> k = m >>= \_ -> k return :: a -> m a return = pure
任何一个 Monad 的实例,都必须满足如下性质:
-
Left identity (左单位律)
-- :: m a :: a -> m b -- ↓↓↓↓↓↓↓↓ ↓ return x >>= h === h x -- ↑↑↑ -- :: m b -
Right identity (右单位律)
-- :: m a :: a -> m a -- ↓↓ ↓↓↓↓↓↓ mx >>= return === mx -- ↑↑ -- :: m a -
Associativity (结合律)
-- :: m a -- ┊┊ :: a -> m b -- ┊┊ ┊ :: b -> m c :: a :: m c -- ↓↓ ↓ ↓ ↓ ↓↓↓↓↓↓↓↓↓ (mx >>= g) >>= h === mx >>= (\x -> g x >>= h) -- ↑↑↑↑↑↑↑↑ ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ -- :: m b :: a -> m c小和尚:
-
这里的三个性质,怎么与通常的
单位律和结合律不太一样呢? -
例如,对于加运算,它的性质可以描述如下:
-
左单位律:
0 + x === x -
右单位律:
x + 0 === x -
结合律:
(x + y) + z === x + (y + z)
-
唐僧:
-
你的直觉是对的
-
下面,我们用一些朝三暮四的小把戏,把 Monad Laws 变换到更规整的形式上
在
Control.Monad模块中,定义了一个运算符>=>:-- The monad-composition operator -- defined in Control.Monad (>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c) -- :: a :: m b :: b -> m c -- ↓ ↓↓↓ ↓ f >=> g = \x -> f x >>= g -- ↑↑↑↑↑↑↑↑↑ -- :: m c-
官方称其为 “the monad-composition operator”
-
因其形状像一条小鱼,所以也被称为 “the fish operator”
-
Left identity
(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c)
f >=> g = \x -> f x >>= g
return x >>= h === h x
<==> (return x >>= h) === h x
<==> (\y -> (return y >>= h)) x === h x
<==> ( return >=> h ) x === h x
<==> ( return >=> h ) === h
<==> return >=> h === h
return是>=>运算的左单位元
Right identity
(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c)
f >=> g = \x -> f x >>= g
mx >>= return === mx
<==> f x >>= return === f x
<==> (\y -> f y >>= return) x === f x
<==> ( f >=> return) x === f x
<==> ( f >=> return) === f
<==> f >=> return === f
return是>=>运算的右单位元
Associativity
(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c)
f >=> g = \x -> f x >>= g
( my >>= g) >>= h === my >>= (\y -> g y >>= h)
<==> ( f x >>= g) >>= h === f x >>= (\y -> g y >>= h)
<==> ( f x >>= g) >>= h === f x >>= ( g >=> h)
<==> (\u -> f u >>= g) x >>= h === f x >>= ( g >=> h)
<==> ( f >=> g) x >>= h === f x >>= ( g >=> h)
<==> (\u -> ( f >=> g) u >>= h) x === (\u -> f u >>= ( g >=> h)) x
<==> (\u -> ( f >=> g) u >>= h) === (\u -> f u >>= ( g >=> h))
<==> ( ( f >=> g) >=> h) === ( f >=> ( g >=> h))
>=>运算满足结合律
唐僧:
- 我时常再想,“朝三暮四” 是一个贬义词吗?
08 Monad Laws 在实践中的价值
do { x' <- return x; f x' }
=== return x >>= \x' -> f x'
=== return x >>= f -- 根据 left identity law, 可知:
=== f x
=== do { f x }
do { x <- mx; return x }
=== mx >>= \x -> return x
=== mx >>= return x -- 根据 right identity law, 可知:
=== mx
=== do { mx }
do { y <- do { x <- mx; f x }; g y }
=== do { x <- mx; f x } >>= \y -> g y
=== (mx >>= \x -> f x ) >>= \y -> g y
=== (mx >>= f ) >>= g -- 根据 associativity law, 可知:
=== mx >>= (\x -> f x >>= g)
=== do { x <- mx; do { y <- f x; g y} }
=== do { x <- mx; y <- f x; g y }
skip_and_get = do unused <- getLine
line <- getLine
return line
根据 right identity law,可知:
skip_and_get = do unused <- getLine
getLine
main = do answer <- skip_and_get
putStrLn answer
把 skip_and_get 的定义代入:
main = do answer <- do { unused <- getLine;
getLine }
putStrLn answer
根据 associativity law,可知:
main = do unused <- getLine
answer <- getLine
putStrLn answer
这些 law 根本不是什么约束,而是天然就应该存在的
09 Monad as Computation
给定 monad M,可将类型 M a 的一个值 “理解为” 一种计算,且计算结果是若干类型为 a 的值
对于类型为 a 任何一个值 x,存在一种 “do nothing” 的计算,它只是简单地返回 x:
return :: (Monad m) => a -> m a
对于任何一对计算 mx :: m a 和 my :: m b,存在对两者的一种顺序组合:
(>>) :: (Monad m) => m a -> m b -> m b
- 在这种顺序组合中,第一步的计算结果会被抛弃
存在一种 “根据第一步的计算结果决定第二步的计算” 的组合计算:
(>>=) :: (Monad m) => m a -> (a -> m b) -> m b
-
mx >>= f :: m b- 在这个组合计算中,首先计算
mx,然后根据计算结果x确定下一步计算f x
- 在这个组合计算中,首先计算
例如:
main :: IO ()
main = getLine >>= putStrLn
main :: IO ()
main = putStrLn "Enter a line of text:"
>> getLine >>= \x -> putStrLn (reverse x)
在更一般的场景中,通过 >> 和 >>=,可能会形成非常长的计算链条。
为了让这种长计算链条在形式上更简洁,Haskell 提供了 do 语法。
例如,上面的程序可以改写为如下形式:
main :: IO ()
main = do
putStrLn "Enter a line of text:"
x <- getLine
putStrLn (reverse x)
do与>>>>=的相互变换do { x } === xdo { x ; <stmts> } === x >> do { <stmts> }do { v <- x ; <stmts> } === x >>= \v -> do { <stmts> }do { let <decls> ; <stmts> } === let <delcs> in do { <stmts> }
>> 与 >>= 不仅仅是顺序组合
-
上面的解释,将
>>与>>=描述为计算的顺序组合 -
但真实情况并非如此:
-
>>与>>=的真实组合行为由具体的 monad 实例确定 -
在不同的 monad 实例上,
>>与>>=可能会表现出截然不同的组合行为
-
Control.Monad 中的若干示例
sequence :: (Monad m) => [m a] -> m [a]
sequence [] = return []
sequence (x:xs) = do
v <- x
vs <- sequence xs
return (v:vs)
main = sequence [getLine, getLine] >>= print
forM :: (Monad m) => [a] -> (a -> m b) -> m [b]
forM xs f = sequence $ map f xs
main = forM [1..10] $ \x -> do
putStr "Looping: "
print x
when :: (Monad m) => Bool -> m () -> m ()
when p mx = if p then mx else return ()
10 课堂练习
练习 01
给定如下的树结构 (数据存放在非叶子节点中):
data Tree a = Leaf | Node (Tree a) a (Tree a) deriving (Show)
将它声明为 Functor 的一个实例:
instance Functor Tree where
-- fmap :: (a -> b) -> Tree a -> Tree b
fmap g Leaf = Leaf
fmap g (Node l x r) = Node (fmap g l) (g x) (fmap g r)
练习 02
在 Haskell 中,给定两个类型 X Y,运算符 -> 可以构造出一个新的类型 X -> Y。因此:
ctor (->) : Type -> Type -> Type
而且,在 Haskell 中,X -> Y 确实可以被等价地写为 (->) X Y
显然可知:
(->)不可能成为Functor的实例。但是:
(->) a有可能成为Functor的实例;因为ctor (->) a :: Type -> Type
请将 (->) a 声明为 Functor 的实例:
instance Functor ((->) a) where
-- fmap :: (a -> b) -> f a -> f b // 这里的 a 与 上面的 a 重名了;因此,改名
-- fmap :: (b -> c) -> f b -> f c
-- fmap :: (b -> c) -> (->) a b -> (->) a c
-- fmap :: (b -> c) -> (a -> b) -> (a -> c)
fmap = (.)
练习 03
请将 (->) a 声明为 Applicative 的实例:
instance Applicative ((->) a) where
-- pure :: a -> f a
-- pure :: b -> f b
-- pure :: b -> a -> b
pure = const
-- (<*>) :: f (a -> b) -> f a -> f b
-- (<*>) :: f (b -> c) -> f b -> f c
-- (<*>) :: (a -> b -> c) -> (a -> b) -> (a -> c)
g <*> h = \x -> g x $ h x
本章作业
作业 01
请将
(->) a声明为Monad的实例:
作业 02
给定如下类型定义:
data Expr a = Var a | Val Int | Add (Expr a) (Expr a) deriving Show
请将
Expr声明为FunctorApplicativeMonad的实例通过一个示例,解释
Expr上的操作>>=的行为
第 13 章:Monadic Parser
01 什么是解析器 (Parser) ?
解析器是一个程序:它接收一段文本信息 (即,一个字符串),对其进行分析,确定其语法结构 (Syntactic Structure)
例如,对于字符串 2 * 3 + 4,一个特定的解析器可能会把它理解为如下的树形结构:
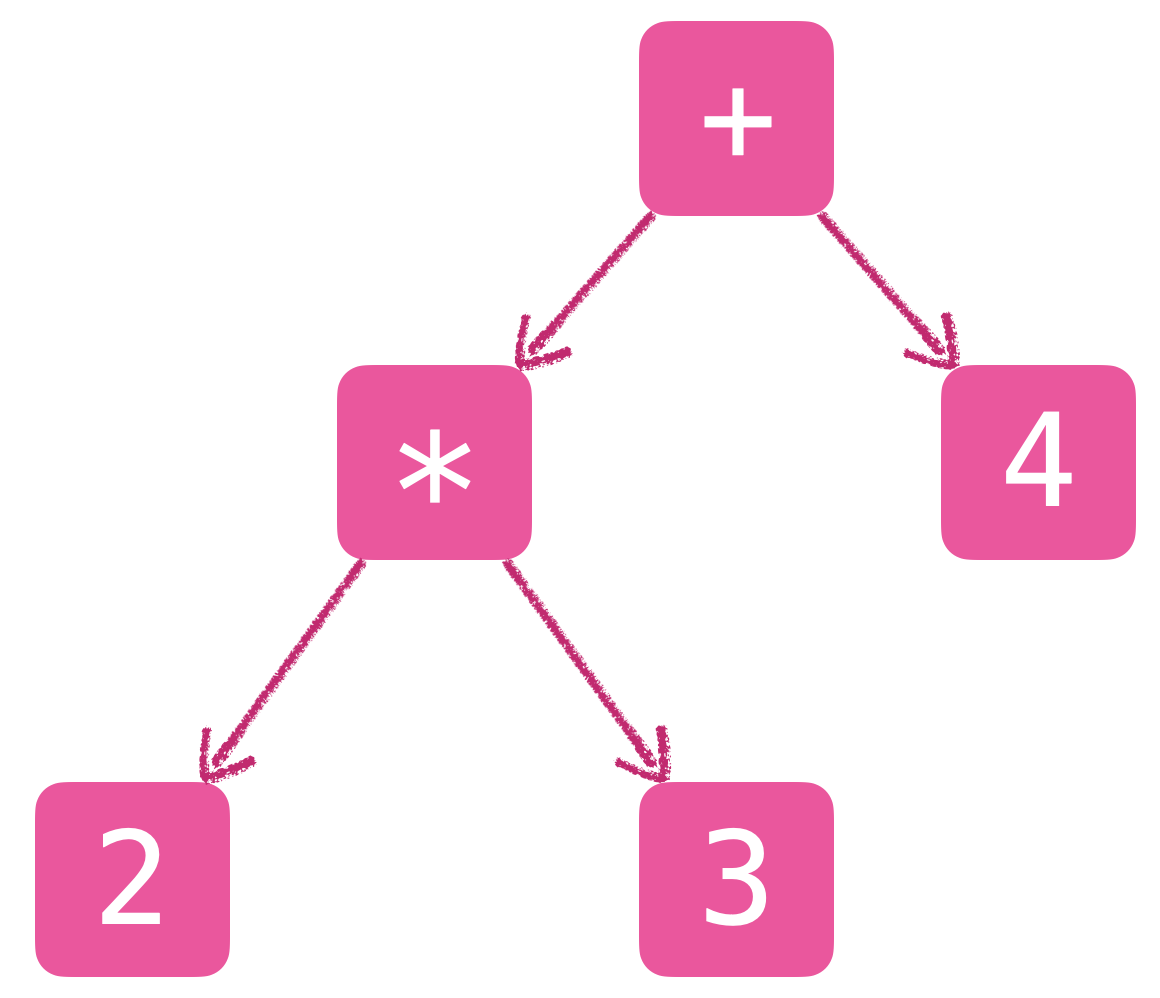
02 在哪里会用到解析器 ?
目前看来,任何一种程序设计语言,它的工具链中大概都会存在一个解析器。
举例而言:
-
你在 ghci 中输入的字符串 (Haskell 程序/表达式),需要经过一个解析器进行分析后,才会进行后续处理
-
你在 终端 (Terminal) 中输入的命令 (也是一种程序),也是如此
-
在浏览器中打开一个页面,本质上是打开一个使用 HTML 语言编写的程序,将这个程序解析为一棵 DOM (Document Object Model) 树,然后再把这棵树渲染在浏览器窗口中
-
你现在正在浏览的这个页面,它的本质是一个使用 markdown 语法撰写的程序;这个程序在被解析后被转换为 HTML 程序,然后再被浏览器解析和渲染,然后才被你看到
03 将解析器建模为函数
type Parser = String -> Tree
- 解析器是一个函数:它接收一个字符串,返回一种树形结构
一般情况下,解析器的输出是一棵树,称为 抽象语法树 (Abstract Syntax Tree / AST)
在更一般的情况下,我们需要表示 “部分解析”:
- 即,只解析了输入字符串的一个前缀 (余下的部分仍然是一个字符串)
type Parser = String -> (Tree, String)
-
解析器的返回值是一个二元组
(Tree, String)-
已被解析的部分被表示为一棵树
-
未被解析的部分仍然保持字符串的形态
-
在更为复杂的情况下,可能会解析失败,也可能存在多种不同的解析方式:
type Parser = String -> [(Tree, String)]
-
解析器的返回值是一个序列
[(Tree, String)]-
当解析失败时,返回序列的长度为
0 -
当只存在一种解析方式时,返回序列的长度为
1 -
当存在
n种解析方式时,返回序列的长度为n
-
然后,我们可以将解析器的输出泛化为任何一种类型:
type Parser a = String -> [(a, String)]
- 在本章中,我们只考虑解析器的返回序列长度为
0或1这两种情况
最后,为了能够将 Parser 声明为 Monad 的实例,对 Parser 进行如下定义:
newtype Parser a = P (String -> [(a,String)])
顺便定义一个 app 函数,将一个解析器作用到一个程序上:
app :: Parser a -> String -> [(a,String)]
app (P f) = f
下面,我们就来实现各种各样的解析器。
04 The item Parser
item :: Parser Char
item = P $ \program -> case program of
[] -> []
(x:xs) -> [(x, xs)]
itemparser 仅从程序中取出第一个字符
ghci> app item ""
[]
ghci> app item "abc"
[('a',"bc")]
05 将 Parser 声明为 Monad 的实例
instance Functor Parser where
-- fmap :: (a -> b) -> Parser a -> Parser b
fmap g p = P $ \program -> case app p program of
[] -> [] -- 遇到失败,则传播/返回失败
[(v, out)] -> [(g v, out)]
ghci> app (toUpper <$> item) "abc"
[('A',"bc")]
ghci> app (toUpper <$> item) ""
[]
instance Applicative Parser where
-- pure :: a -> Parser a
pure v = P $ \program -> [(v,program)]
-- <*> :: Parser (a -> b) -> Parser a -> Parser b
pg <*> px = P $ \program -> case app pg program of
[] -> [] -- 遇到失败,则传播/返回失败
[(g, out)] -> app (g <$> px) out
ghci> app (pure 1) "abc"
[(1,"abc")]
ghci> three = g <$> item <*> item <*> item where g x y z = (x,z)
ghci> app three "abcdef"
[(('a','c'),"def")]
instance Monad Parser where
-- (>>=) :: Parser a -> (a -> Parser b) -> Parser b
p >>= f = P $ \program -> case app p program of
[] -> []
[(v, out)] -> app (f v) out
ghci> app (return 1) "abc"
[(1,"abc")]
ghci> three = do { x <- item; item; z <- item; return (x, z) }
ghci> app three "abcdef"
[((‘a','c'),"def")]
06 选择 (Choice)
在模块 Control.Applicative 中定义了一个类簇:
-- A monoid on applicative functors.
class Applicative f => Alternative f where
-- An associative binary operation
-- 一个满足结合律的二元运算符
(<|>) :: f a -> f a -> f a
-- The identity of '<|>'
-- 二元运算符 '<|>' 的单位元
empty :: f a
-- Zero or more.
many :: f a -> f [a]
many v = some v <|> pure []
-- One or more.
some :: f a -> f [a]
some v = (:) <$> v <*> many v
-
<|>满足结合律x <|> (y <|> z) === (x <|> y) <|> z -
empty是<|>的单位元empty <|> x === xx <|> empty === x
将 Maybe 声明为 Alternative 的实例
instance Alternative Maybe where
-- empty :: Maybe a
empty = Nothing
-- (<|>) :: Maybe a -> Maybe a -> Maybe a
Nothing <|> r = r -- 若第一个选择为空,则返回第二个选择
l <|> _ = l -- 若第一个选择非空,则返回第一个选择
-- 以下代码无需书写;放在这里,只为方便阅读和理解
-- Zero or more.
many :: Maybe a -> Maybe [a]
many v = some v <|> pure []
-- ^^^^^^^
-- === Just []
-- 如果 some v 为 Nothing,则返回 Just [];表示 zero 次
-- 否则,返回 some v;表示 more 次
-- One or more.
some :: Maybe a -> Maybe [a]
some v = (:) <$> v <*> many v
-- 若 v 为 Nothing,则返回 Nothing
ghci> import Control.Applicative
ghci> some Nothing
Nothing
ghci> many Nothing
Just []
将 Parser 声明为 Alternative 的实例
instance Alternative Parser where
-- empty :: Parser a
empty = P $ \program -> []
-- 一个直接返回失败的解析器
-- (<|>) :: Parser a -> Parser a -> Parser a
p <|> q = P $ \program -> case app p program of
[] -> app q program
rst -> rst
-- 对于输入的程序,首先用 p 进行解析:
-- 如果解析失败,则用 q 进行解析,并返回解析的结果
-- 否则,返回用 p 进行解析的结果
--
-- 简而言之,p <|> q 的效果是:
-- 如果一个程序用 p 能够成功解析,则 p <|> q === p
-- 否则,p <|> q === q
--
-- 这样,就实现了一种顺序尝试的效果:
-- 即,顺序尝试若干解析方式
-- 遇到第一个成功的解析方式,则返回该解析结果
-- 否则,返回最后一种解析方式的结果 (无论成功或失败)
-- 以下代码无需书写;放在这里,只为方便阅读和理解
-- Zero or more.
many :: Parser a -> Parser [a]
many v = some v <|> pure []
-- ^^^^^^^
-- === P $ \program -> [([],program)]
--
-- 对输入的程序尽可能多地连续使用 v 进行解析
-- 若一次都没有成功,则不进行任何解析
-- One or more.
some :: Parser a -> Parser [a]
some v = (:) <$> v <*> many v
-- 首先,对输入的程序使用 v 进行一次解析
-- 若发生失败,则返回/传播失败
-- 然后,再对余下未被解析的程序 使用 many v 进行解析
ghci> app empty "abc"
[]
ghci> app (item <|> return 'd') "abc"
[('a',"bc")]
ghci> app (empty <|> return 'd') "abc"
[('d',"abc")]
07 若干基础解析器
sat :: (Char -> Bool) -> Parser Char
sat p = do
x <- item
if p x then return x else empty
-- 或者
sat p = item >>= \x -> if p x then return x else empty
-
sat p把两个动作组合在一起-
首先,解析出程序中的第一个字符
x -
然后,如果
x满足谓词p,-
则返回
x以及余下未被解析的程序 -
否则,返回失败
-
-
-- 数字字符解析器
digit :: Parser Char
digit = sat isDigit
-- 小写字母解析器
lower :: Parser Char
lower = sat isLower
-- 大写字母解析器
upper :: Parser Char
upper = sat isUpper
-- 字母解析器
letter :: Parser Char
letter = sat isAlpha
-- 字母或数字解析器
alphanum :: Parser Char
alphanum = sat isAlphaNum
-- 指定字符解析器
char :: Char -> Parser Char
char x = sat (x ==)
课堂练习:
定义一个解析器:
string :: String -> Parser String分析输入的程序是否具有一个制定的前缀。
string的行为示例如下:ghci> app (string "abc") "abcdef" [("abc","def")] ghci> app (string "abc") "ab1234" [] ghci> app (string "") "ab1234" [("","ab1234")]#![allow(unused)] fn main() { string :: String -> Parser String string [] = return [] string (x:xs) = do char x string xs return (x:xs) }
08 The ident Parser / 标识符解析器
我们将一个标识符 (identifier) 定义为满足如下条件的字符串:
-
字符串的首字符必须是一个小写英文字母
-
除首字符之外的其他字符,或者是英文字母,或者是数字
ident :: Parser String
ident = do
x <- lower
xs <- many alphanum
return (x:xs)
ghci> app ident "abc def"
[("abc"," def")]
ghci> app ident "12 def"
[]
09 The nat Parser / 自然数解析器
nat :: Parser Int
nat = do
xs <- some digit
return (read xs)
ghci> app nat "123abc"
[(123,"abc")]
ghci> app nat "abc123"
[]
10 The space Parser / 空格字符解析器
space :: Parser ()
space = do
many (sat isSpace)
return ()
ghci> app space " abc"
[((),"abc")]
11 The int Parser / 整数解析器
int :: Parser Int
int = do char '-'
n <- nat
return $ - n
<|> nat
ghci> app int "123abc"
[(123,"abc")]
ghci> app int "-123abc"
[(-123,"abc")]
ghci> app int "abc123"
[]
12 在解析过程中,去除首尾空格
token :: Parser a -> Parser a
token p = do
space
v <- p
space
return v
identifier :: Parser String
identifier = token ident
natural :: Parser Int
natural = token nat
integer :: Parser Int
integer = token int
symbol :: String -> Parser String
symbol xs = token $ string xs
13 The nats Parser
nats :: Parser [Int]
nats = do
symbol "["
n <- natural
ns <- many $ do {symbol ","; natural}
symbol "]"
return (n:ns)
ghci> app nats "[1, 2, 3 ]"
[([1,2,3],"")]
ghci> app nats "[1, 2, 3, ]"
[]
14 算术运算表达式的解析与评估
考虑满足如下条件的表达式:
-
仅包含
个位数、+、*、以及用于优先级控制的圆括号对() -
+和*满足右结合律 -
*的优先级高于+
这种表达式可以使用如下的 上下文无关文法 (Context-Free Grammar) 进行描述
#![allow(unused)] fn main() { expr ::= term '+' expr | term // 一个 expr, // - 或者是:一个 term 后跟一个字符 '+',然后再跟一个 expr // - 或者是:一个 term // // 其中: // - 用单引号包围的字符,称为 终结字符 (即,出现在程序中的固定字符) // - 字符 | 是一种表示 “或” 的结构 // // 上面这一条文法,也可以紧凑地表示为如下形式 expr ::= term ('+' expr | ε) // 其中,ε 表示 “空” term ::= factor '*' term | factor // 类似地,上面这条文法也可写为如下紧凑形式 term ::= factor ('*' term | ε) factor ::= digit | '(' expr ')' digit ::= '0' | '1' | ... | '9' }
下面,我们就把上面的文法依次翻译到对应的解析器上。
#![allow(unused)] fn main() { expr ::= term ('+' expr | ε) }
expr :: Parser Int
expr = do t <- term
do symbol "+"
e <- expr
return (t + e)
<|> return t
#![allow(unused)] fn main() { term ::= factor ('*' term | ε) }
term :: Parser Int
term = do f <- factor
do symbol "*"
t <- term
return (f * t)
<|> return f
#![allow(unused)] fn main() { factor ::= digit | '(' expr ')' }
factor :: Parser Int
factor = do symbol "("
e <- expr
symbol ")"
return e
<|> natural
最后,定义评估函数:
eval :: String -> Int
eval xs = fst $ head $ app expr xs
下面是使用示例:
ghci> eval "2 * ( 3 + 4 )"
14
ghci> eval "2 * 3 + 4"
10
本章作业
作业 01
对本章介绍的算术表达式解析器进行扩展,支持
减 (-)和除 (/)两种运算。具体而言,根据如下两条更新后的文法,对解析器的实现进行相应地修改:
#![allow(unused)] fn main() { expr ::= term ('+' expr | '-' expr | ε) term ::= factor ('*' term | '/' term | ε) }